中学2年数学 式の計算 式の利用 2練習問題2・解答
2、連続する整数の和
連続する3つの整数の和は3の倍数になることを、文字の式を用いて説明してください。
【解答・解説】
nを整数とすると、連続する3つの整数はn,n+1,n+2を表すことができます。
ですから、その和は
n+(n+1)+(n+2)=3n+3
=3(n+1)
ここで、n+1は整数ですから、3(n+1)は3の倍数となります。
よって、連続する3つの整数の和は3の倍数になります。
 数学
数学  化石
化石  数学
数学  式の計算
式の計算  数学
数学  因数分解
因数分解 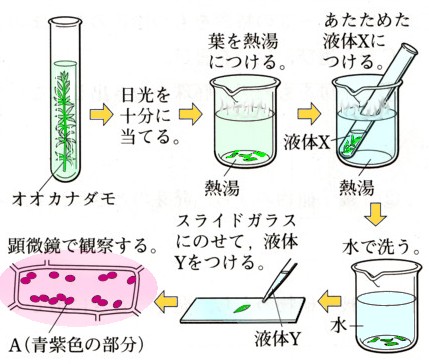 植物
植物 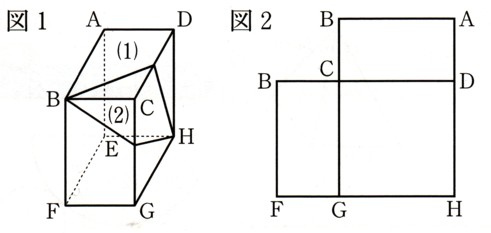 数学
数学  数学
数学  数学
数学  エネルギー
エネルギー  光の世界
光の世界  歴史
歴史  数学
数学 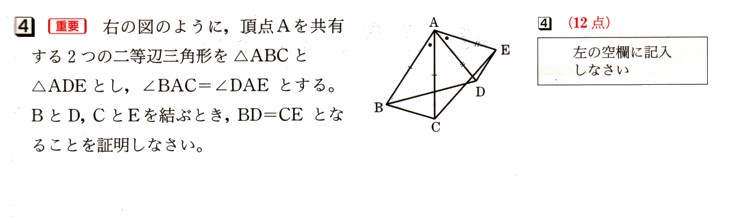 数学
数学 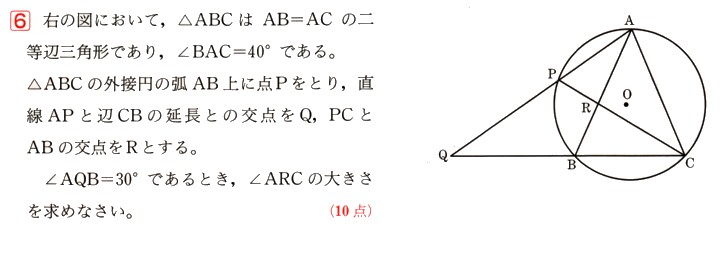 平面図形
平面図形  式の計算
式の計算 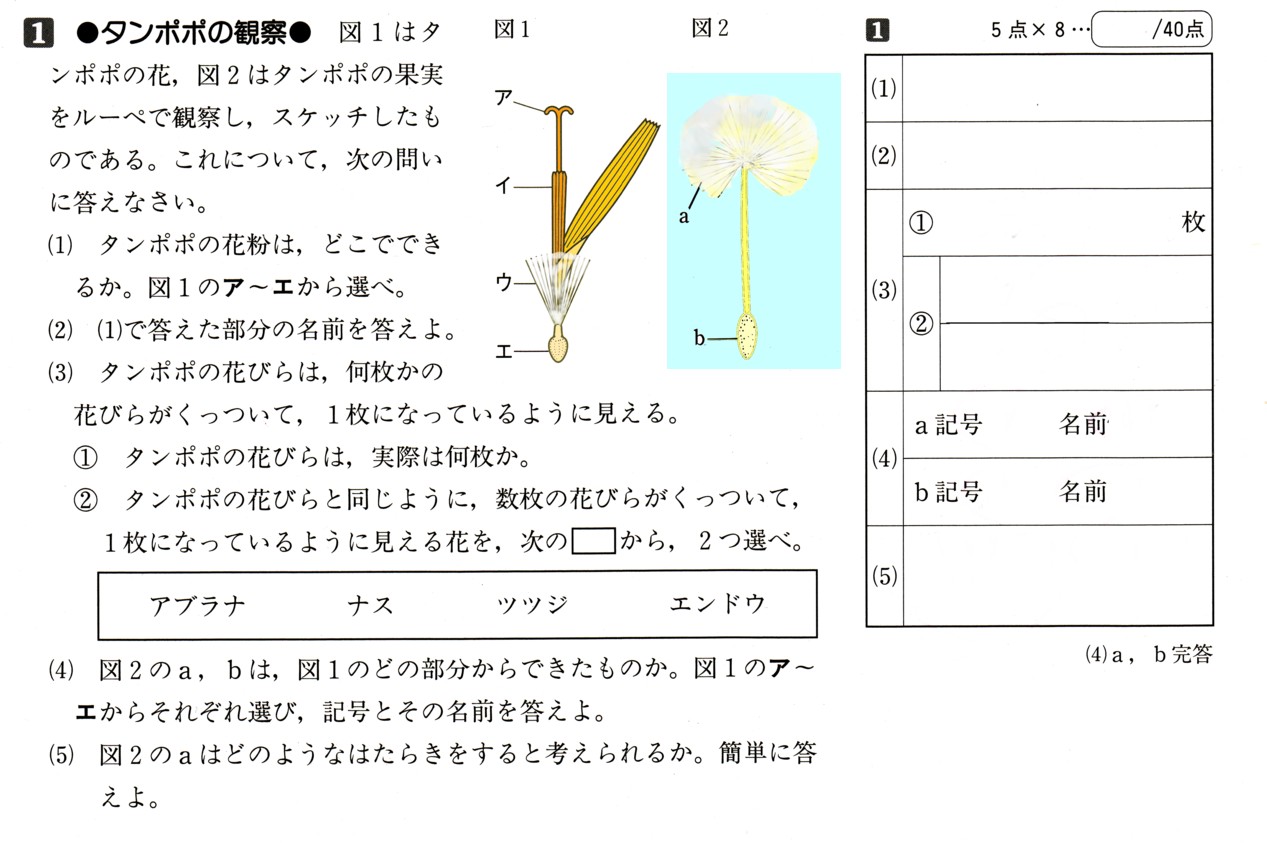 植物
植物  式の利用
式の利用中学2年数学 式の計算 式の利用 2練習問題2・解答
2、連続する整数の和
連続する3つの整数の和は3の倍数になることを、文字の式を用いて説明してください。
【解答・解説】
nを整数とすると、連続する3つの整数はn,n+1,n+2を表すことができます。
ですから、その和は
n+(n+1)+(n+2)=3n+3
=3(n+1)
ここで、n+1は整数ですから、3(n+1)は3の倍数となります。
よって、連続する3つの整数の和は3の倍数になります。
コメント