中学2年数学 平面図形 まとめテスト3・解答
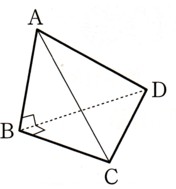
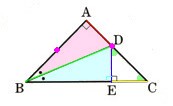
3、∠A=90°、AB=ACである直角三角形ABCがあります。
∠Bの二等分線が辺ACと点Dで交わり、Dから辺BCに垂線DEを引くとき、AD=ECであることを証明してください。
答え 

〔証明〕
△ABDと△EBDにおいて
仮定より
∠DAB(90°)=∠DEB(90°)
ですから直角三角形になります。
辺BDは共通・・・・①
∠ABD=∠EBD・・・・②
直角三角形ですから、
①、②より
斜辺とその他の角がそれぞれ等しくなりますから
△ABD≡△EBD
になります。
合同な三角形の対応する辺はそれぞれ等しくなりますから
AD=ED・・・・③
になります。
つぎに△ECDについて考えます。
∠DECは仮定により90°になります。
∠DEC=90°・・・・④
∠ECDは△ABCの∠BCAと同じになります。
△ABCは二等辺三角形で、∠BCAは、45°ですから、
∠ECD=45°となり
∠CDE=180°ー(90°+45°)
=45°
∠CDE=∠ECD
となり、△ECDは二等辺三角形になります。
二等辺三角形の頂角Eを挟む2つの辺EDと辺ECが等しいことがわかります。
ED=EC・・・・⑤
③、⑤より
AD=DE=EC
になり
AD=ECになります。








コメント