中学2年数学 式と計算 式の加法・減法 2確認問題4・解答
4、次の計算をしてください。
(1)(χ²−2χ−1)+(−2χ²+4)・・・→( )をはずします。
=χ²−2χ−1−2χ²+4 ・・・→同類項をまとめます。
=χ²−2χ²−2χ−1+4
=−χ²−2χ+3
答え −χ²−2χ+3
(2)7a+3b−(2a−b) ・・・→( )をはずします。
=7a+3b−2a+b ・・・→同類項をまとめます。
=7a−2a+3b+b
=5a+4b
答え 5a+4b
(3)(3χ−2y+z)−4(χ/2+y/4−z) ・・・→( )をはずします。
=3χ−2y+z−2χ−y+4z ・・・→同類項をまとめます。
=3χ−2χ−2y−y+z+4z
=χ−3y+5z
答え χ−3y+5z
(4)2χ²−1/3(6χ−3χ²)+2χ ・・・→( )をはずします。
=2χ²−2χ+χ²+2χ ・・・→同類項をまとめます。
=2χ²+χ²−2χ+2χ
=3χ²
答え 3χ²
(5)2(χ−2y)−3(yー2χ) ・・・→( )をはずします。
=2χ−4y−3y+6χ ・・・→同類項をまとめます。
=2χ+6χ−4y−3y
=8χ−7y
答え 8χ−7y
(6)−5a−{b−3(b−2a)}・・・→まずは( )をはずします。
=−5a−{b−3b+6a} ・・・→次に{ }をはずします。
=−5a−b+3b−6a ・・・→同類項をまとめます。
=−5a−6a−b+3b
=−11a+2b
答え −11a+2b








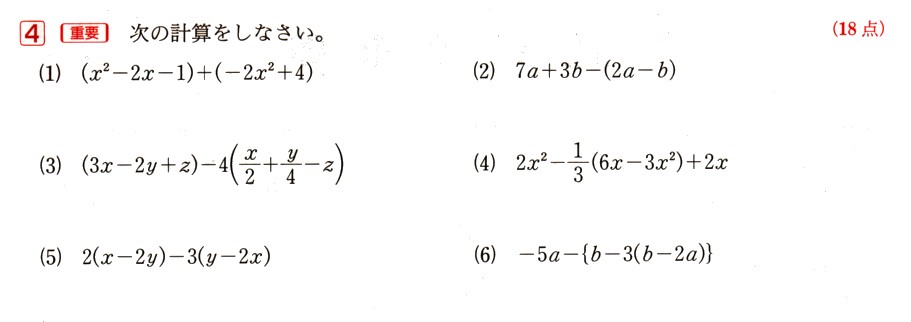
コメント