中学2年数学 1次関数 3まとめテスト1（２）・解答
（３）（2）の操作で満水にする場合と、空の水槽にＢの管だけで給水して満水にする場合とでは、満水になるまでかかる時間の違いは何分間か求めてください。
(2)のグラフの結果。
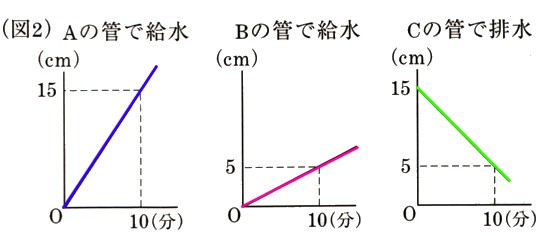
95分で満水になったことがわかります。
管Ｂは、毎分0.5cm溜まる。（傾き）は1/2
式にすると。空の水槽に入れ始めますから。(切片)は無く、原点Ｏから始まることがわかります。
(水槽の深さ)＝(Ｂ管の毎分の水量)×(時間)
ｙ＝1/2 χ
になります。
満水になるまでの時間を求めるのですから
40＝χ/2
χ/2＝40
χ＝80
80分で満水になるとわかります。
満水になる時間の差は、
【(2)の操作の満水時間】−【管Ｂでの満水時間】＝【時間差】
95分 − 80 ＝15(分)
答え 15分間
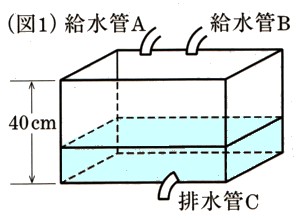
（４）満水の状態から、Ｃの管で排水を始めました。Ｃの管で排水し続けたまま20分後にＢの管で給水を始めました。その20分後にさらにＡの管でも給水を始めました。Ａの管での給水を始めてから15分後の水の深さは何cmになるのか?求めて下さい。（図5を使って考えてください。）
20分間は、40(満水)−20(分)×(毎分１cm、排水量)＝40?−20?＝20?(２０分後の水深)
20～40分間は、排水しながら給水した状態になります。
排水量は、変わりませんから、20(分)×(毎分１cm、排水量)
給水量は、Ｂの管ですから、 20(分)×（毎分0.5cm、給水量）
排水量のほうが多くなっていますから、
(Ｂの毎分の給水量)−(Ｃの毎分の排水量)＝(20分間の毎分の排水量)
0.5cm − 1? ＝ −0.5cm
20～40分間の式は
(時間)×(20分間の毎分の排水量)＝(40分後の水深)
20 × −0.5? ＝ −10cm
(0～20分間の水深)＋(20～40分間の水深)＝(40分後の水深)
20? ＋(−10cm) ＝10cm
40分後からは、排水しながら、A,Bの管から給水も同時にしています。
（Aの毎分の給水量）毎分1.5?
(Bの毎分の給水量) 毎分0.5?
（Aの毎分の給水量）＋(Bの毎分の給水量)＝（A,Bの毎分の給水量）
毎分1.5? ＋ 毎分0.5? ＝ 毎分2cm
(Cの毎分の排水量) 毎分１cm
（A,Bの毎分の給水量）−(Cの毎分の排水量)＝(40から55分までの毎分の給水量)
毎分2cm
コメント