中学3年数学 関数y=aχ² まとめテスト5・解答
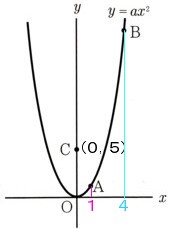
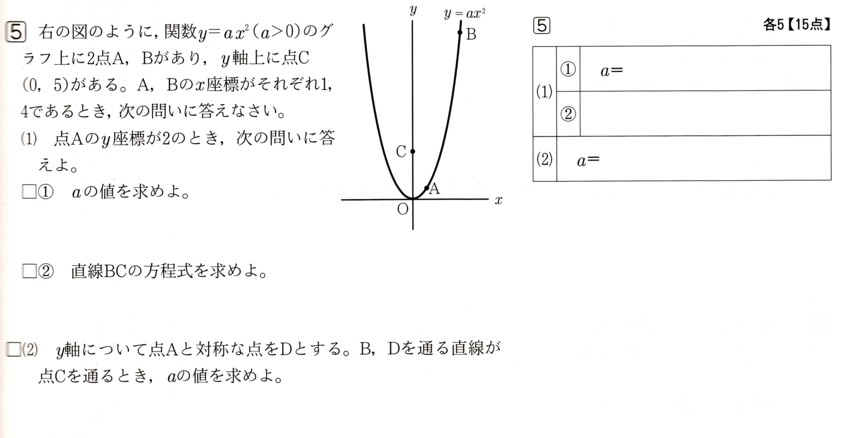
5、図 のように、関数y=aχ²(a>0)のグラフ上に2点A,Bがあります。y軸上に点C(0,5)があります。
のように、関数y=aχ²(a>0)のグラフ上に2点A,Bがあります。y軸上に点C(0,5)があります。
A,Bのχ座標がそれぞれ1,4であるとき、次の問いに答えてください。
(1)点Aのy座標が2のとき、次の問いに答えてください。
y=aχ²
点A(1,2),点B(4,b)
点C(0,5)
?aの値を求めてください。
y=aχ²にχ=1、y=2を代入します。
2=a(1)²
2=a
答え a=2
?直線BCの方程式を求めてください。
直線BCは右上がりですから、
y=aχ+b
点Cの座標が(0,5)ですから切片は5になります。
y=aχ+5
次にBの座標を求めます。
Bの座標はy=2χ² にχ=4を代入します。
y=2(4)²
y=2×16
y=32
Bの座標は(4、32)になります。
直線BCの式を求めるために、y=aχ+5に(4、32)を代入します。
32=4a+5
4a=32−5
4a=27
a=27/4
傾き(27/4)、切片(5)がわかりましたから、直線BCの式は
y=27/4χ+5
になります。
答え y=27/4χ+5
(2)y軸について点Aと対称な点をDとします。B,Dを通る直線が点Cを通るとき、aの値を求めてください。
まずは、点Dの座標は(−1,a)になります。
点Bの座標は(4,b)になり、点Cの座標は(0,5)になります。
点Bのχ座標4をy=aχ²に代入します。
y=a(4)²
y=16a
点Bの座標は(4、16a)になります。
点B、点C、点Dは一直線上にありますから、
DC,CBの傾きは同じになります。
直線の式の傾きは、変化の割合になります。
yの増加量
変化の割合=――――― になります。
χの増加量
ですから、
DCの変化の割合=CBの変化の割合
点Dの座標は(−1,a)
点Cの座標は(0,5)
点Bの座標は(4、16a)
5−a 16a−5
―――― = ――――
0−(−1) 4−0
5−a 16a−5
――=―――
1 4
4(5−a)=16a−5
20−4a=16a−5
16a+4a=20+5
20a=25
25 5
a=――=――
20 4
答え a=5/4








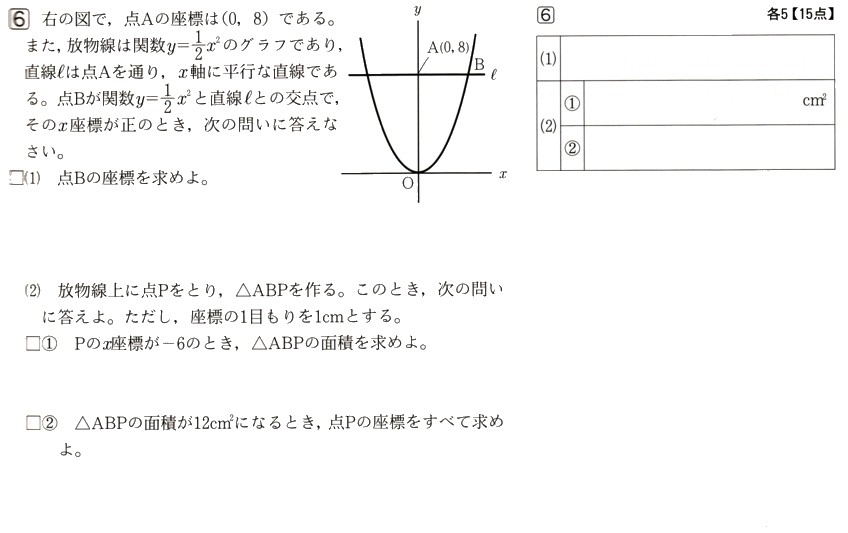
コメント