中学2年数学　連立方程式　いろいろな連立方程式　確認問題1･解答

中学2年数学　連立方程式　いろいろな連立方程式　確認問題1･解答

１、やや複雑な連立方程式

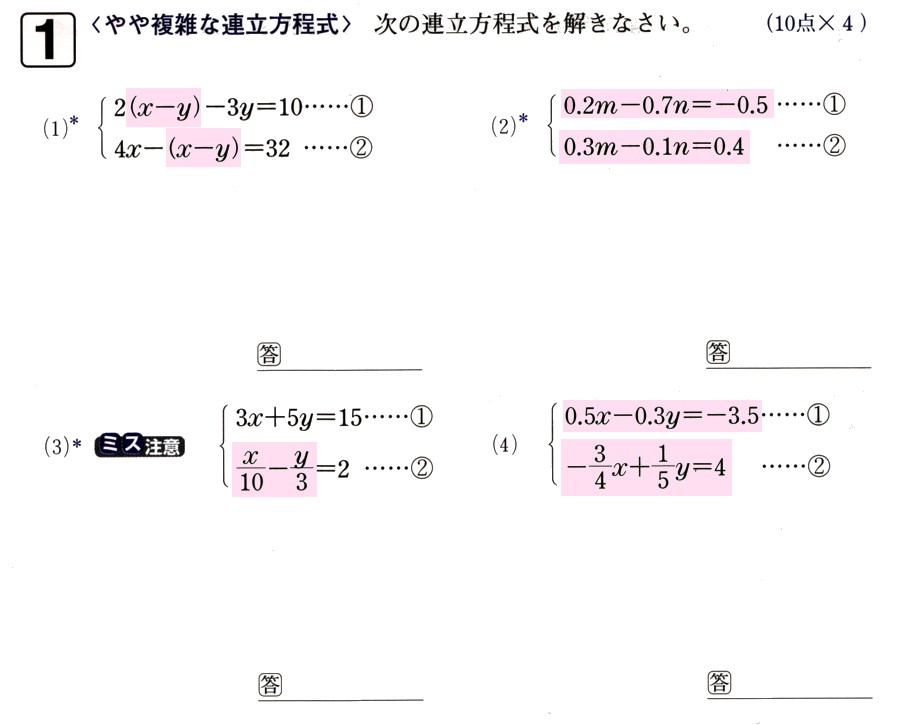
　　次の連立方程式を解いてください。

　　　　　2（χ−y）−3y＝10　　・・・?
（１）｛
　　　　　4χ−（χ−y）＝32　　・・・?

        2χ−2y−3y＝10
      {
        4χ−χ＋y＝32

        2χ−5y＝10  を3倍にして
      {
        3χ＋ y＝32　を2倍にします。

　　　　6χ−15y＝30
　　−）6χ＋ 2y＝64
              −17y＝−34

　　y＝2

　　3χ＋ y＝32　に　y＝2　を代入します。

　　　3χ＋ 2＝32

　　　3χ＝32−2

　　　3χ＝30

　　　　χ＝10

　　　　答え　χ＝10　、　y＝2

　　　　　0.2m−0.7n＝−0.5　・・・?
（２）｛
　　　　　0.3m−0.1n＝0.4　　・・・?

　　　　0.2m−0.7n＝−0.5　を10倍します。
　　　{
　　　　0.3m−0.1n＝0.4　を10倍します。

　　　　2m−7n＝−5　　を3倍します。
　　　{
　　　　3m−1n＝4　　　を2倍します。

　　　　6m−21n＝−15
　　｛
　　　　6m−2n＝8

　　　　6m−21n＝−15
　　−) 6m− 2n＝   8
              −19n＝−23

   n＝23/19

    3m−1n＝4 に　n＝23/19　を代入します。

　　　3m−1（23/19）＝4

　　　3m−23/19＝4

　　　3m＝4＋23/19

　　　19×3m＝19×(4＋23/19）

　　　57m＝76＋23
　　
　　　57m＝99

　　　　m＝99/57　

　　　　m＝33/19

　　　答え　m＝33/19　、 n＝23/19

　　　　　3χ＋5y＝15　　　　・・・?
（３）｛
　　　　　χ/10 − y/3＝2　　・・・?

　　　　χ/10 − y/3＝2　　の分母をそろえます。

　　　　30×(χ/10 − y/3)＝30×2

　　　　　3χ−10y＝60　　・・・?

　　　　　3χ＋5y＝15　　 ・・・?
　　　｛
　　　　　3χ−10y＝60　　・・・?

         3χ＋ 5y＝15
    −)  3χ−10y＝60
                   15y＝−45

      y＝−3

    3χ＋5y＝15 に　y＝−3　を代入します。

　　　3χ＋5（−3）＝15

　　　3χ−15＝15

　　　3χ＝15＋15

　　　3χ＝30

　　　　χ＝10

　　　　答え　χ＝10　、y＝−3

　　　　　0.5χ−0.3y＝−3.5　　　　・・・?
（４）｛
　　　　　−3/4 χ　＋ 1/5 y ＝4　　・・・?

　　　　　0.5χ−0.3y＝−3.5　　　を10倍します。
　　　｛
　　　　　−3/4 χ　＋ 1/5 y ＝4　両辺の分母をそろえます。

　　　　　5χ−3y＝−35　
　　　｛
　　　　　20×(−3/4 χ　＋ 1/5 y) ＝20×4　

　　　　　5χ−3y＝−35　　　を3倍します。
　　　｛
　　　　　−15χ＋4y＝80　

　　　　　　15χ−9y＝−105
　　　＋）−15χ＋4y＝　 80
                      −5y＝−25

        y＝5

      5χ−3y＝−35　に　y＝5　を代入します。

　　　5χ−3（5）＝−35

　　　5χ−15＝−35

　　　5χ＝−35＋15

　　　5χ＝−20

　　　　χ＝−4

　　　　答え　χ＝−4　、 y＝5