中学2年数学 1次関数 1次関数の応用 確認問題2・解答
2、
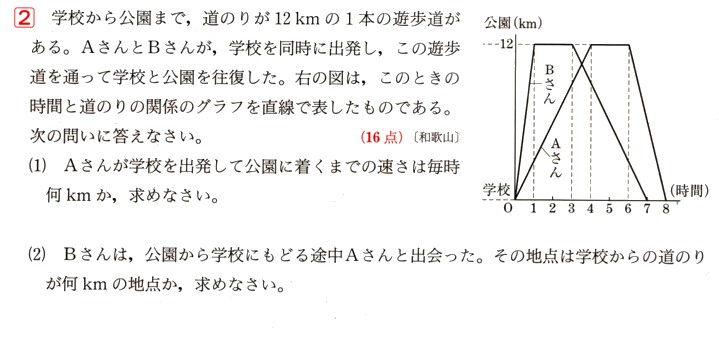
学校から公園まで、道のりが12kmの1本の遊歩道があります。
AさんとBさんが、学校を同時に出発し、この遊歩道を通って学校と公園を往復しました。
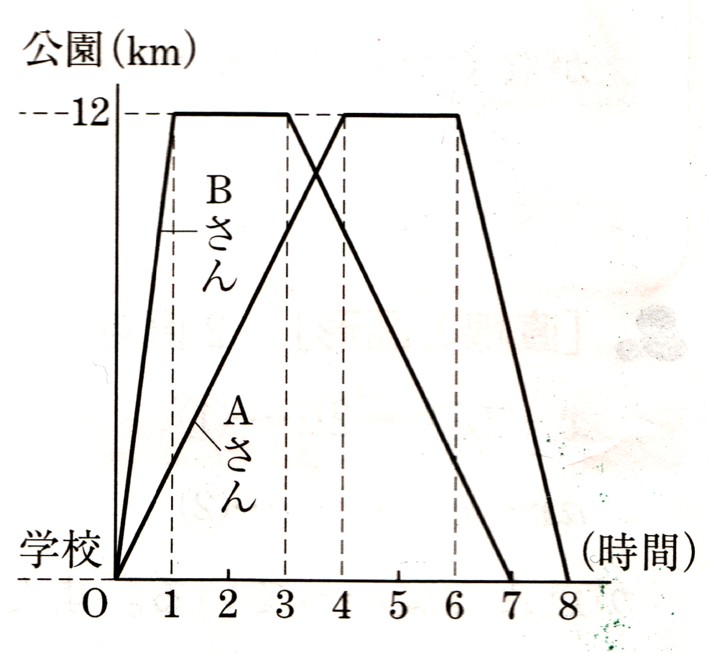
次の図 は、このときの時間と道のりの関係をグラフで表したものになります。
は、このときの時間と道のりの関係をグラフで表したものになります。
次の問いに答えて下さい。
(1)Aさんが学校を出発して公園に着くまでの速さは毎時何kmになりますか?
グラフを見ると、Aさんは、公園まで(12km)を、4時間かかって着いたのですから、速さは
(速さ)=(距離)÷(時間)
=12(?)÷4(時間)
=3
Aさんは、毎時3kmの速さで進んだことがわかります。
答え 毎時3km
(2)Bさんは、公園から学校に戻る途中Aさんと出会いました。その地点は学校からの道のりが何?の地点になりますか?求めて下さい。
y軸=(距離)
χ軸=(時間)
とすると
y=~ の形の式にすると、
(距離)=(速さ)×(時間)
y =Aさんの速さ×χ
y =Bさんの速さ×χ
Aさんの速さは、毎時3kmとわかっていますから、
y=3χ ・・・・Aさん
つぎにBさんの速さを求めます。
y=aχ+b の式にあてはめてみると
12=3a+b (Bさんの公園出発)
{
0=7a+b (Bさんの学校到着)
3a+b=12
−) 7a+b=0
−4a =12
a=−3
12=3a+b に a=−3 を代入します。
12=3(−3)+b
12=−9+b
−9+b=12
b=12+9
b=21
y=~の形にします。
y=−3χ+21 ・・・・Bさん
になります。
AさんBさんの2直線の交わる場所が、出会った距離と時間になります。
2直線の交わる場所を求めるために、連立方程式をつくって、わかったχ、yが距離と時間になります。
たずねているのは、出会った距離ですから、yがわかればいいということになります。
y=3χ
{
y=−3χ+21
y=−3χ+21 に y=3χ を代入します。
(3χ)=−3χ+21
3χ+3χ=21
6χ=21
χ=7/2
y=3χ に χ=7/2 を代入します。
y=3(7/2)
y=21/2
y=10.5(?)
となり、出会った距離は学校からみて10.5?の地点になります。
答え 10.5?









コメント