中学1年数学 直線図形と対称 基本の作図 確認問題5 解答・解説
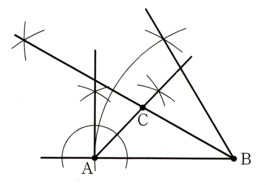
図のような2点A,Bが与えられています。これを用いて、∠A=45゜、
∠B=30゜となる△ABCを1つ作図してください。
まず、点Aと点Bを直線でつなぎます。直線ABに垂直で点Aを通る線を
作図します。
点Aを中心に円をかきます。つぎに、かいた円と直線ABの接点を中心
に半径が同じ円を2つかきますその交点と、点Aを直線で結びます。
これで辺ABに垂直な線がひけました。∠Aは45゜ですから、90゜の
半分になります。ですからできた?の二等分線を作図すれば45゜になります。
それでは点Aにできた、∠90゜の二等分線を作図します。点A を中心に適当な
円をかきます、その円と接した辺ABと点Aからの垂線の接点を中心に半径が
同じの円をかきその交点を結びます。その交点と点Aをつなげた直線が45゜に
なります。
次に∠Bについて考えます。∠30ということは???
今まで出習った作図の仕方では垂線(90゜)か、2等分線になります。90゜を3分の1
にするのは???それならば、2等分線になります。∠30゜の2倍は60゜に
なります。60゜は、△ABC’で考えるなら正三角形になります。
[正三角形の1つの角(60゜)の二等分線が30゜になりす。]
それでは、正三角形を作図していきます。
点A,点Bをそれぞれ中心に、半径は辺ABと同じ長さで2つの円をかきます。
2つの円の交点を直線でつなぎます、これで正三角形△ABC’ができました。
∠Bの二等分線を作図すれば60゜の半分の30゜の角がわかります。
∠Bの二等分線を作図していきます。
点Bと中心に適当な円をかき、辺BC’、辺ABと接した部分を中心に半径の
同じ円をかきます。その円の交点と点Bを直線で結んだ線が30゜の線になりま
す。
できた点Aから伸びた線と、点Bから伸びた線との交点が点Cになります。








コメント