中学2年数学 連立方程式 まとめテスト８・解答
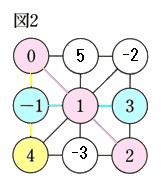
８、図1は、「縦、横、斜めに並んだ3つの数の和をすべて等しくします。」 という決まりによって、○の中に数を入れたものです。
これについて、次の問いに答えて下さい。
（１）この決まりに従って、図2のア～ウにあてはまる数を書いて下さい。
まずは、合計はいくつになるか、を考えます。
上段の左から斜めを考えていきます。
0＋1＋2＝3
になりますから、この問題のルールは、「縦、横、斜めに並んだ3つの数の和は3、ということになります。」
イ、ウ のどちらか、から考えます。
イ、4＋1＋χ＝3 、2＋3＋χ＝3
χ＝3−5
χ＝−2
イ＝−2
とわかりました。
次に、ウを考えます。
4＋ｙ＋2＝3
ｙ＝3−6
ｙ＝−3
ウ＝−3
とわかりました。
イとウをそれぞれ図に書き込みます。
次にアを考えます。
上の段の左から
0＋ｚ＋（−2）＝3 、ｚ＋1＋（−3）＝3
ｚ＝3＋2
ｚ＝5
ア＝5
答え ア 5 、イ −2 、ウ −3、
（２）図3はこの決まりに従って、６つの○に式や数を入れたものです。連立方程式を使って、χ、ｙにあてはまる数を求めて下さい。
縦の右の列で考えましょう。
2χ＋7＋ｙ
上の列の右から斜めに
2χ＋（χ＋3）＋6
＝2χ＋χ＋3＋6
＝3χ＋9
下の列は
6＋（ｙ＋5）＋ｙ
＝6＋ｙ＋5＋ｙ
＝2ｙ＋11
になります。
3χ＋9＝2χ＋7＋ｙ
｛
2ｙ＋11＝2χ＋7＋ｙ
3χ−2χ−ｙ＝7−9
｛
2χ＋ｙ−2ｙ＝11−7
χ−ｙ＝−2
｛
2χ−ｙ＝4
χ−ｙ＝−2
−）2χ−ｙ＝ 4
−χ ＝−6
χ＝6
2χ−ｙ＝4 に χ＝6 を代入します。
2（6）−ｙ＝4
12−ｙ＝4
−ｙ＝4−12
−ｙ＝−8
ｙ＝8
答え χ＝6 、ｙ＝8
（３）（2）の結果をもとに、図3のア～ウにあてはまる数を書いて下さい。
ア～ウ以外の○の中に数字を書き込んでいきます。
2χ＝2×6＝12
χ＋3＝6＋3＝9
ｙ＋5＝8＋5＝13
ｙ＝8
縦の右の列の合計を考えます。
12＋7＋8＝27
になります。
イ、ウから考えていきます。
イ＋9＋13＝27
イ＝27−22
イ＝5
ウ＋9＋7＝27
ウ＝27−16
ウ＝11
イ、ウ に書き込んでみましょう。
アは、
ア＋5＋12＝27 、ア＋11＋6＝27
ア＝27−17
ア＝10
答え ア、10 イ、5 ウ 11
お疲れ様でした！
コメント