中学3年数学 ｙ＝ａχ²の値の変化 ２確認問題１・解答
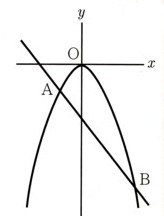
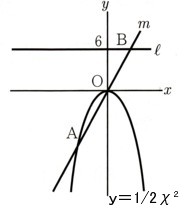
１、図
の放物線は関数ｙ＝−1/2χ²のグラフであり、ℓは（０，６）を通りχ軸に平行な直線になります。
また、mは放物線と原点および点Aで交わります。直線ℓとは点Bで交わる直線になります。点Aの
χ座標が−4であるとき、次の問いに答えてください。
（１）関数y＝−1/2χ²について、χが−4から0まで増加するときの変化の割合を求めてください。
y＝−1/2χ²にχ=−4、χ=0を代入します。
y＝−1/2（−４）² 、y＝−1/2（０²）
ｙ＝−1/2×１６ 、ｙ＝０
ｙ＝−８
ｙの増加量 ０−（−８） ８
変化の割合＝――――――＝―――――＝――＝２
χの増加量 ０−（−４） ４
答え ２
（２）直線ℓ上にAB＝AC となる点Cをとるとき、次の問いに答えてください。
?2点A,Cを通る直線の式をy＝aχ＋ｂとするとき、ａ、ｂの値を求めてください。
点Aのχ座標はy＝−1/2（χ）²で、χ＝−４を代入するとｙ座標は−８
y＝−1/2（−４）²
＝−８
ｙ＝aχ にχ＝−４、ｙ＝−８を代入すると
−８＝−４a
４a＝８
ａ＝２
直線mの傾きは２とわかりましたから直線mの式は
ｙ＝２χ
点Aの座標は（−４、−８）
点Bの座標は、ｙ＝２χにｙ＝６を代入します。
６＝２χ
２χ＝６
χ＝３
点Bの座標は（３，６）になりました。
直線ACの中点までの距離は３＋４＝７
中点から、点Cのχ座標は−４＋（−７）＝−１１
になり、点Cの座標は（−１１，６）となります。
直線ACの式は左から右下がりになりますから（−）になます。
ｙ＝−ａχ＋ｂ
点A（−４、−８）と点C（−１１，６）の座標を式に代入します。
−８＝−４a＋ｂ
｛
６＝−１１a＋ｂ
（加減法）
６＝−１１a＋ｂ
−）−８＝−４a＋ｂ
１４＝−７ａ
−７ａ＝１４
ａ＝−２
６＝−１１a＋ｂ にａ＝−２ を代入します。
６＝−１１×（−２）＋ｂ
６＝２２＋ｂ
ｂ＝６−２２
ｂ＝−１６
傾きと切片がわかりました。
直線ACの式はｙ＝−２χ−１６ になります。
答え ａ＝−２、ｂ＝−１６
?関数ｙ＝−1/2χ²のグラフ上に、△ＰＢＣの面積が△ＡＢＣの面積の1/2となるような点Ｐをとります。
このとき、点Ｐの座標を求めてください。ただし、Ｐのχ座標は正になります。
まずは△ＡＢＣの面積を考えます。
底辺をＢＣと考えると１４
高さは直線ＢＣの中点で考えれば８＋６＝１４ になります。
１４×１４÷２＝９８
直線ＢＰが直線ＣＢの半分であれば面積は△ＡＢＣの半分になります。
９８÷２＝４９
点Ｐのｙ座標は点Ｂからの垂線がｙ＝−１/２χ²に接する部分ですから、
点Ｐのｙ座標は６−７＝−１ になります。
χを求めるためにｙ＝−１/２χ²にｙ＝−１を代入します。
−１＝−１/２χ²
１/２χ²＝１
χ²＝２
χ＝√２
点Ｐの座標
がわかりました。
答え （χ、ｙ）＝（√２、−１）
コメント