中学３年数学 式の展開と因数分解 式の計算の利用 ２確認問題３・解答
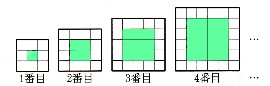
３、図
のように、同じ大きさの白と黒の正方形のタイルを隙間なく重ならないように規則正しく並べ，太い線で囲まれた図形をつくっていきます。このとき，次の問いに答えてください。
のように、同じ大きさの白と黒の正方形のタイルを隙間なく重ならないように規則正しく並べ，太い線で囲まれた図形をつくっていきます。このとき，次の問いに答えてください。 まずは、図を見てわかることを考えていきましょう。
を見てわかることを考えていきましょう。 ｎ番目 緑のタイルの枚数 白いタイルの枚数 １列のタイルの数 合計のタイルの枚数
１番目 １²＝１ （１＋２）²ー１²＝８ （１＋２）＝３ （１＋２）²＝９
２番目 ２²＝４ （２＋２）²ー２²＝１２ （２＋２）＝４ （２＋２）²＝１６
３番目 ３²＝９ （３＋２）²ー３²＝１６ （３＋２）＝５ （３＋２）²＝２５
４番目 ４²＝１６ （４＋２）²ー４²＝２０ （４＋２）＝６ （４＋２）²＝３６
・
・
ｎ番目 ｎ² （ｎ＋２）²ーｎ² （ｎ＋２） （ｎ＋２）²
（１）ｎ番目の図形には，緑のタイルは何枚使われていますか？ｎの式で表してください。
ｎ番目の２乗が緑のタイルの数になります。
ｎ²（枚）となります。
答え ｎ²（枚）
（２）ｎ番目の図形には，白いタイルは何枚使われていますか？ｎの式で表してください。
白いタイルは、ｎ番目の合計のタイルの数から緑のタイルの数を引いたのが白いタイルの数になります。
（ｎ番目のすべてのタイルの数）ー（ｎ番目の緑のタイルの数）＝（ｎ番目の白いタイルの数）
（ｎ＋２）² ー ｎ² ＝（ｎ＋２）²ーｎ²
答え （ｎ＋２）²ーｎ² （枚）
（３）白いタイルが１２０枚使われている図形には，緑のタイルは何枚使われていますか？
（ｎ＋２）²ーｎ² ＝１２０
乗法公式を利用します。
●（ａ＋ｂ）²＝ａ²＋２ａｂ＋ｂ²
ｎ²＋４ｎ＋４ーｎ²＝１２０
ｎ²ーｎ²＋４ｎ＋４＝１２０
４ｎ＋４＝１２０
４ｎ＝１２０ー４
４ｎ＝１１６
ｎ＝１１６／４
ｎ＝２９
ｎは何番目を表しますから、２９番目になります。
緑のタイルの数を求めるには、
ｎ²＝（緑のタイルの数）
２９²＝（３０ー１）²
＝３０²ー２×1×３０＋１²
＝９００−６０＋１
＝８４１
答え ８４１（枚）
コメント