中学2年数学 連立方程式 2練習問題6・解答
6、整数の問題
*十の位の数がχ、一の位の数がy、2桁の整数は、10χ+y
2桁の整数がある。各位の数の和が13で、十の位の数と一の位の数を入れ替えると、元の整数よりも27大きくなるといいます。
十の位の数をχ、一の位の数をyとして連立方程式をつくり、もとの整数を求めて下さい。
? 十の位の数が χ、
一の位の数が y
足した答えが 13
ですから、
(十の位の数)+(一の位の数)=13
χ y
χ+y=13
? 入れ替えた式で考えます。
十の位の数が 10×y
一の位の数が χ
(10y+χ)
になります。
もとの整数より27大きい
もとの整数は、2桁ですから
10の位+1の位 になります、
10の位はχ×10
1の位は y
(10χ+y) となり。
27より大きくなりますから
(10χ+y)+27
(入れ替えた整数)=(もとの整数+27)
(10y+χ) = (10χ+y)+27
連立方程式をつくります。
χ+y=13
{
10y+χ=(10χ+y)+27
χ=−y+13
{
10y+χ=10χ+y+27
10y−y+χ−10χ=27
9y−9χ=27
9(y−χ)=27
y−χ=3
y−χ=3 に χ=−y+13 を代入します。
y−(−y+13)=3
y+y−13=3
2y=3+13
2y=16
y=8
χ+y=13 に y=8 を代入します。
χ+(8)=13
χ=13−8
χ=5
χは十の位の数で、yは一の位の数になりますから
58 になります。
答え χ+y=13
{ ・ もとの整数 58
10y+χ=(10χ+y)+27




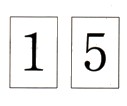








コメント