中学2年数学 図形の調べ方 図形の合同 確認問題7・解答
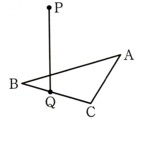
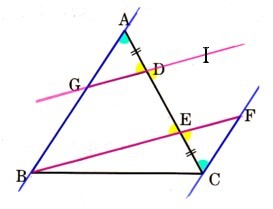
7、図 のように、△ABCにおいて、辺AC上にAD=CEとなるように2点D、Eをとります。BEの延長と、点Cを通り辺ABに平行な直線との交点をFとします。また、点Dを通りBFに平行な直線と辺ABとの交点をGとします。このとき、△AGD≡△CFEであることを証明してください。
のように、△ABCにおいて、辺AC上にAD=CEとなるように2点D、Eをとります。BEの延長と、点Cを通り辺ABに平行な直線との交点をFとします。また、点Dを通りBFに平行な直線と辺ABとの交点をGとします。このとき、△AGD≡△CFEであることを証明してください。
答え
[証明] 
△AGDと△CFEにおいて、
仮定により
AD=CE・・・?
AB//CF ですから、
錯角により
∠BAC=∠ACF・・・?
同位角により
∠CEF=∠BED・・・?
同位角により
∠ADG=∠EDI・・・?
GD//BF ですから、
錯角により
∠BED=∠EDI・・・?
?、?、?より
∠ADG=∠CEF・・・?
?、?、?より
1辺と、その両端の角がそれぞれ等しくなります。
よって、
△AGD≡△CFE
になります。












コメント