中学3年数学 図形と相似 平行線と線分の比 3確認問題1・解答
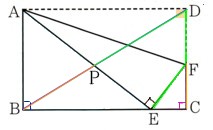
1、次の図 は、長方形ABCDの紙片を、頂点Dが辺BC上の点Eに重なるように、
は、長方形ABCDの紙片を、頂点Dが辺BC上の点Eに重なるように、
線分AFを折り目として折ったときの図になります。このとき、次の問いに答えてください。
(1)△ABE∽△ECFであることを次のように証明しました。[ ]a~cをうめて
証明を完成してください。
[証明]
△ABEと△ECFで、
四角形ABCDは長方形ですから、
∠[a ]=∠ECF・・・?
∠AECは△ABEの頂点Eにおける[b ]だから、
∠AEC=∠[a ]+∠BAE・・・?
また、∠AEC=∠AEF+∠[c ]・・・?
ここで、∠[a ]=∠AEFだから、
?,?より、∠BAE=∠[c ]・・・?
?,?より、2組の角が、それぞれ等しいので、
△ABE∽△ECF
答え
[証明]
△ABEと△ECFで、
四角形ABCDは長方形ですから、
∠[a・ABE]=∠ECF・・・?
∠AECは△ABEの頂点Eにおける[b・外角]だから、
∠AEC=∠[a・ABE]+∠BAE・・・?
また、∠AEC=∠AEF+∠[c・CEF]・・・?
ここで、∠[a・ABE]=∠AEFだから、
?,?より、∠BAE=∠[c・CEF]・・・?
?,?より、2組の角が、それぞれ等しいので、
△ABE∽△ECF
a・ABE、b・外角、c・CEF
(2)元の長方形ABCDの対角線BDと線分ABとの交点をPとするとき、PD:PB=FD:FC
であることを証明してください。
答え
[証明]
長方形ですから
AD//BE になります。
ですから、
PD:PB=AD:EBとなります。
△PAD∽△PEB になります。
つぎに、 △AEFと△ADFは合同な三角形になりますから
△AEFと△ADFは合同な三角形になりますから
AE=AD
になり、 PD:PB=AE:EB・・・?
PD:PB=AE:EB・・・?
(1) より、△ABE∽△ECFですから、
より、△ABE∽△ECFですから、
AE:EB=EF:FC・・・?
となります。
△AEF=△ADF ですから
辺EFと辺FDは同じになります。
EF=FD・・・?
?,?,?より
PD:PB=FD:FC
となります。










コメント