中学1年数学 立体の表面積と体積 練習問題1 解答・解説
図の立体の表面積と体積をそれぞれ求めてください。
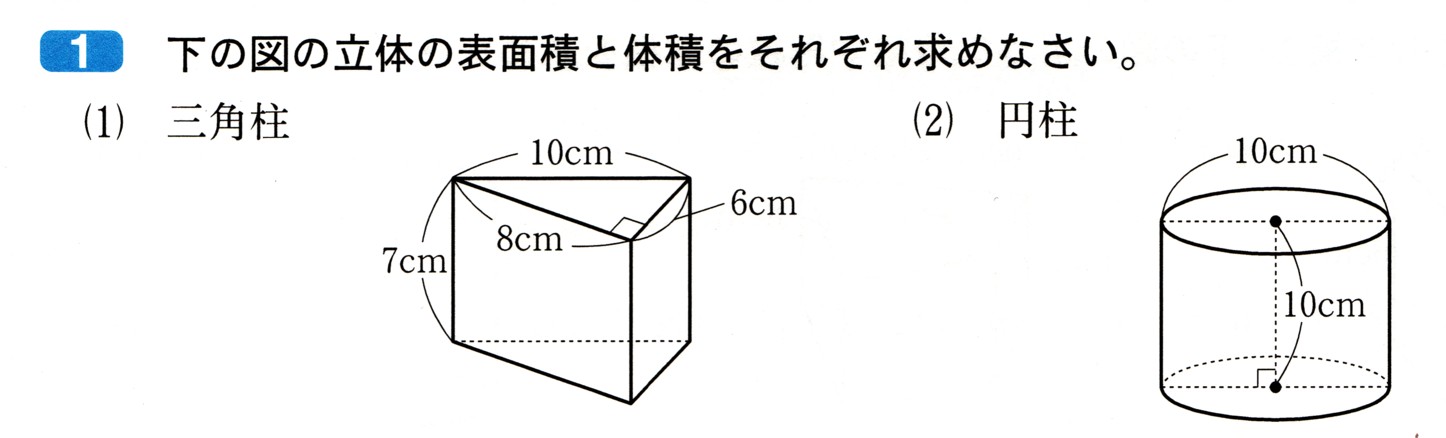
(1)三角柱
まずは、表面積から考えていきましょう。
この三角柱を展開図で考えます。
表面積は、 底面積・・・?上底
{ ?下底
側面積
からできています。
上底と下底は、同じ面積なので、どちらか1つの面で考えます。
底面の形は、三角形ですから
三角形の面積を求めます。
三角形の面積を求める式は
S=(底辺)×(高さ)×1/2
になります。
底辺を6cmと考えると
高さは、8cmになります。
(三角形の面積)=6cm×8cm×1/2
=24cm²
上底と下底は、同じ面積ですから。
(上底)=(下底)
24cm²×2=48?²
これで、底面の面積がわかりました。
次に、側面の面積を考えます。
側面は、長方形の形になりますから、
長方形の面積の求め方は、
1辺×1辺=(長方形の面積)
1辺は、三角柱の高さになりますから、7? になります。
もう1辺は、底面の三角形の周の長さになります。
三角形の周の長さは、それぞれの辺を足せばわかりますから。
10cm+6cm+8cm=24cm
これで、2つの辺の長さがわかりました。
(長方形の面積)=7?×24cm
=168cm²
(三角柱の表面積)=(上底)+(下底)+(側面積)
=(底面積)×2+(側面積)
=48?²+168cm²
=216?²
つぎに、三角柱の体積を求めます。
三角柱の体積を求める式は
V=Sh
(三角柱の体積)=(底面積)×(高さ)
底面積は、三角形で上の表面積で、わかっていますから
底面積は、24cm²
高さは、7?
(三角柱の体積)=24cm²×7?
=168cm³
答え 表面積 216?² 、体積 168cm³
(2)円柱
まずは、表面積から考えていきましょう。
この円柱を展開図で考えます。
表面積は、底面積・・・?上底
{ ?下底
側面積
からできています。
上底と下底は、同じ面積なので、どちらか1つの面で考えます。
底面の形は、円ですから
円形の面積を求めます。
円形の面積を求める式は
S=πγ²
(円の面積)=(半径)×(半径)×π
になります。
円柱の底面の円の直径が、10cmですから
半径は5cmということがわかります。
=5cm×5cm×π
=25πcm²
底面積=(上底)+(下底)
=25π+25π 〈(25π)×2〉
=50πcm²
次に側面積を考えます
側面は長方形になりますから
1辺×1辺になります
1つの辺は、円柱の高さになりますから
10cmになります。
次のもう1辺を考えます
もう1つの辺は、底面の円の円周の長さになります。
円周を求める式は
(円周)=2πγ
=2×半径×π
半径は、5cmですから
=2×5×π
=10πcm
(円周)=(側面の1辺に長さ) ですから
(側面の1辺に長さ)=10πcm
これで2つの辺の長さがわかりました。










コメント