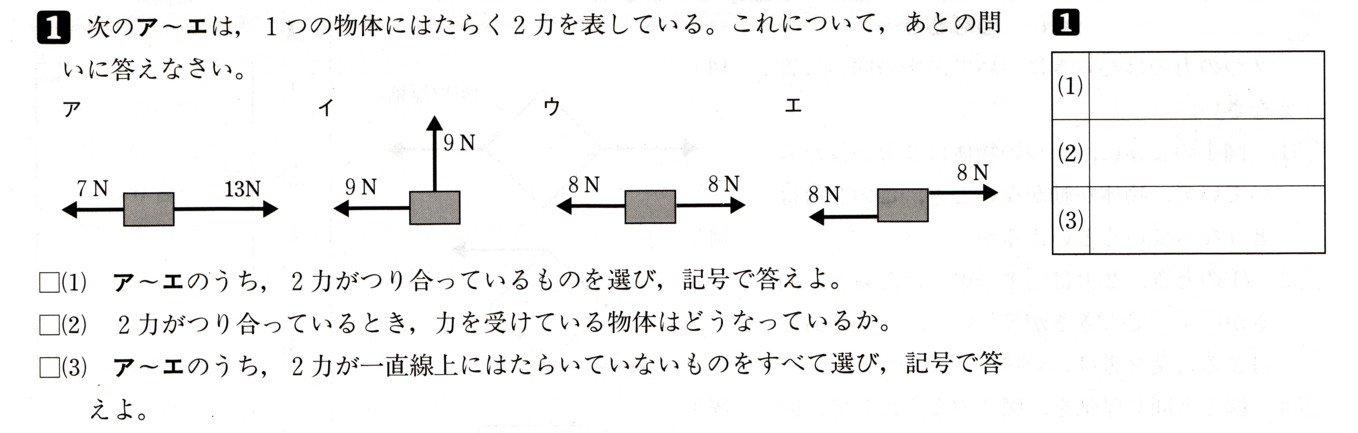
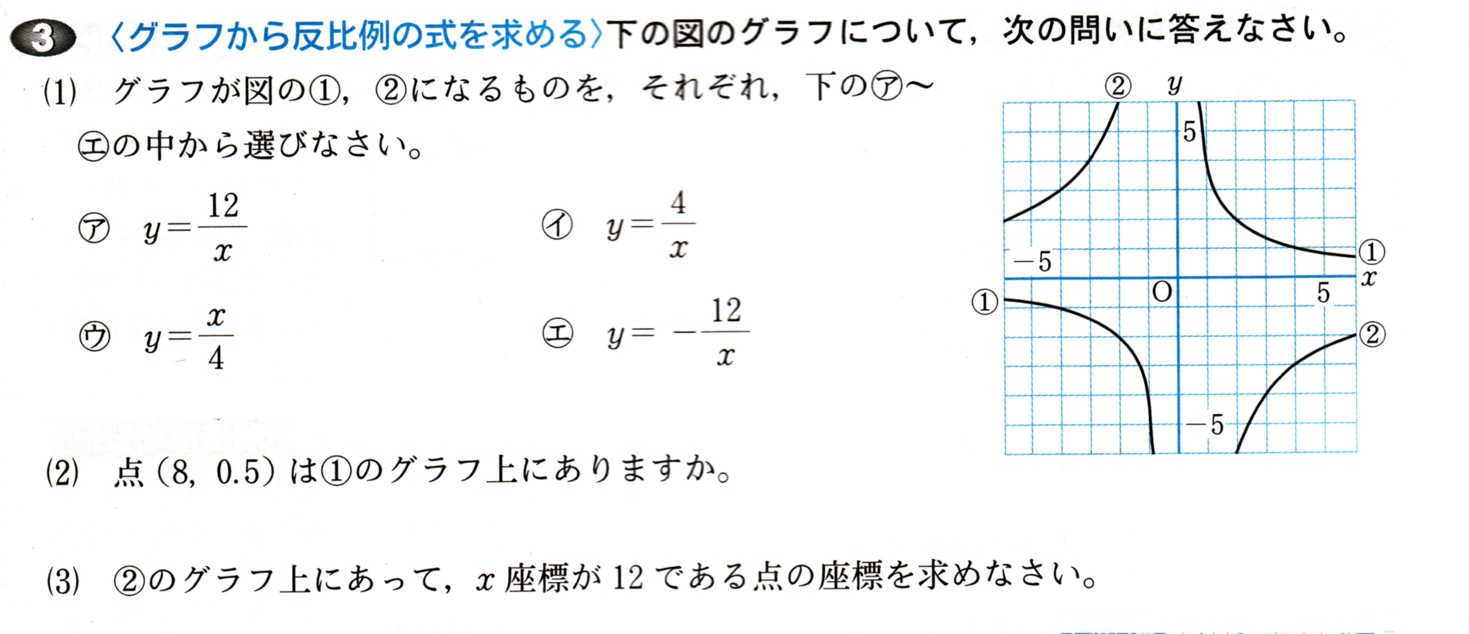
中学2年数学　連立方程式　２練習問題2・解答

中学2年数学　連立方程式　２練習問題2・解答

２、鶴亀算

　　　鶴と亀が合わせて32匹おります。足の数が全部で90本になります。鶴の数をχ、亀の数をｙとします。次の問いに答えて下さい。

（１）鶴と亀の合計について、方程式をつくって下さい。

　　鶴は、χ(匹)

　　亀は、ｙ(匹)

　　合計は、32(匹)

　　　ですから、

　　　鶴＋亀＝32

　　　χ＋ｙ＝32

　　　　答え　χ＋ｙ＝32

（２）足の数の合計について、方程式をつくって下さい。

　　　　一羽の鶴の足の数は、2本

　　　　1匹の亀の足の数は、4本

　　　（一羽の鶴の足の数）×（鶴の数）＝（鶴の足の合計の数）
　　　　　　　2(本)　　　　　χ(羽)　　　       　　2χ(本)
　　　　　　

　　　　（1匹の亀の足の数）×（亀の数）＝（亀の足の合計の数）
　　　　　　　4(本)　　　　　　ｙ(匹)　　　         　4ｙ(本)

　　　（鶴の足の合計の数）＋（亀の足の合計の数）＝90
　　　　　　2χ(本)　　　　　　　           4ｙ(本)

　　　　答え　2χ＋4ｙ＝90

（３）(1)、(2)の連立方程式を解いて、鶴と亀の数を求めて下さい。

　　　　χ＋ｙ＝32
　　｛
　　　　2χ＋4ｙ＝90

　　　χ＋ｙ＝32

　　　χ＝−ｙ＋32

　　　　2χ＋4ｙ＝90　に　χ＝−ｙ＋32　を代入します。

　　　　2（−ｙ＋32）＋4ｙ＝90

　　　　−2ｙ＋64＋4ｙ＝90

　　　　−2ｙ＋4ｙ＝90−64

　　　　　2ｙ＝26

　　　　　ｙ＝13

　　　　χ＋ｙ＝32　に　ｙ＝13　を代入します。

　　　　χ＋13＝32

　　　　χ＝32−13

　　　　χ＝19

　　　χは、鶴で、亀はｙですから、
　

　　　　答え　　鶴19羽　、亀13匹