中学1年数学　円とおうぎ形　確認問題7　解答・解説

中学1年数学　円とおうぎ形　確認問題7　解答・解説

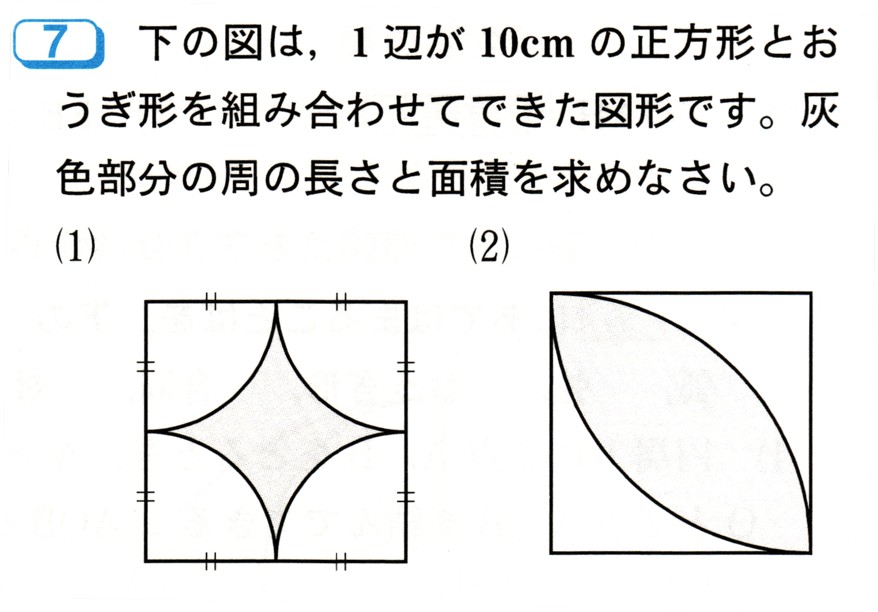
 　図は、1辺が10cmの正方形とおうぎ形を組み合わせてできた図形です。灰色の

　部分の周の長さと面積を求めてください。

（１）この図形の灰色の部分は、1辺が10cmの正方形の面積から4つのおうぎ形を

　　ひいた面積になります。

　　　この4つのおうぎ形を足すと、1つの円になります。この円の半径は5?にな

　　ります。

　　　まずは、円の面積を求めましょう。

　　円の面積の求め方は。S＝πγ²

　　(円の面積)＝π×半径×半径

　　　　　　　＝π×5×5

　　　　　　　＝25π

　　　(円の面積)＝25π(?²)

　　正方形の面積は

　　1辺×1辺ですから

　　10×10＝100

　　　　(正方形の面積)＝100(?²)

　　　　(正方形の面積)−(円の面積)＝(灰色部分の面積)

　　　　　100(?²)　　−25π(?²)＝　75(?²)

　　次に、灰色部分の周の長さを求めます

　　この。灰色部分の周の長さは、おうぎ形の弧の長さになります。

　この4つの弧の長さの合計は円の円周の長さに等しくなりますから。

　　円の円周を求めれば灰色部分の周の長さになります。

　　それでは、円の周の長さを求めましょう。

　　円の周を求める式は

　　ℓ＝2πγ

　　(円周)＝2×π×半径

　　　　　＝2×π×5

　　　　　＝10π

　　　これで、円の周の長さがわかりました。円の周の長さは、灰色部分の

　　周の長さになりますから

　　灰色部分の周の長さは　10πcm　になります

　　　答え　面積　75(?²)　、周の長さ　10π(cm)

（２）

　　この図形の灰色の部分の求め方は、　2つのおうぎ形でできます。この扇形の

　　弧の長さを求めれば、灰色部分の周の長さを求めることができます。

　　弧の長さの求め方は

　　　ℓ＝2πγ×中心角/360

　　　(弧の長さ)＝2×π×半径×中心角/360

　　　　　　　　＝2×π×10×90/360

　　　　　　　　＝5π

　　　今求めたのは1つのおうぎ形の弧の長さですから、同じ長さの弧の長さが

　　2つありますから、2×5π　になり

　　10πcmになります。

　　　次に、灰色部分の面積を求めます

　　考え方とすれば、正方形の面積からおうぎ形の面積をひけば、1つの白い部分に

　　なります。弧の白い部分が2つありますから最後に2倍にすれば白い部分の面積

　　が求められます。そして、正方形の面積から、白い部分の合計の面積をひけば、

　　　灰色の部分の面積を求めることができます。

　　　
　　それでは考えていきましょう。

　　　まずは正方形の面積を求めます

　　正方形の面積は、1辺×1辺ですから

　　　10×10＝100?²

　　　次におうぎ形の面積を求めます。

　　おうぎ形の面積の求める式は

　　　S＝πγ²×中心角/360

　　ですから

　　　わかっている

　　　　半径　　10cm

　　　　中心角　90゜

　　をあてはめていきます

　　　　(おうぎ形の面積)＝π×半径×半径×中心角/360

　　　　　　　　　　　　＝π×10×10×90/360

　　　　　　　　　　　　＝25πcm²

　　　(正方形の面積)−(おうぎ形の面積）＝(残りの面積)

　　　　100?²　　−　　πcm²　　　　　＝　　　　　　

　　残りの面積は2つありますから

　　2×(100?²ー25π?²)＝200-50π?²

　　(正方形の面積)−(残りの面積の合計)＝100?²−(200?²−50π?²)

　　　　　　　　　　　　　　　　　　　＝100−200＋50π(?²)　

　　　　　　　　　　　　　　　　　　　＝50π−100(?²)

　　　になります。

　　　答え　　周の長さ　10πcm　、面積　50π−100(?²)