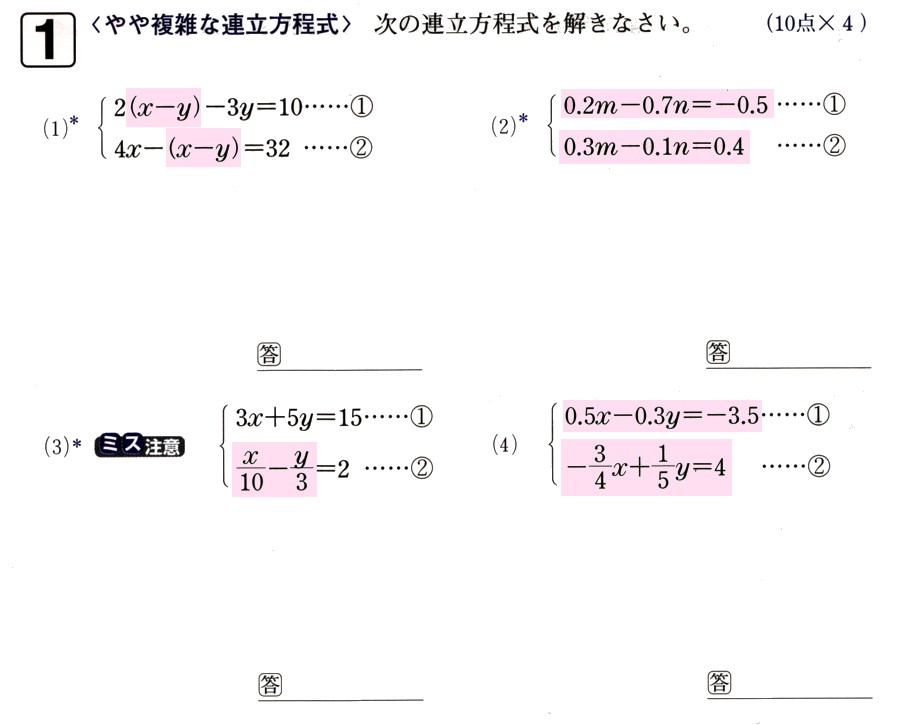
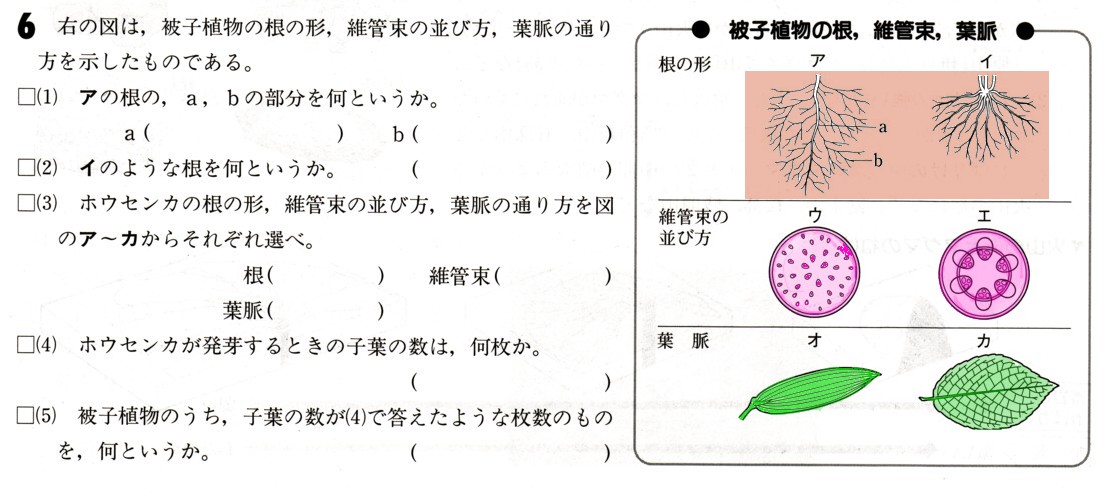
中学2年数学 図形の調べ方 三角形・多角形と角 確認問題3・解答
３、次の問いに答えてください。
（１）△ＡＢＣにおいて、∠Ａの大きさは∠Ｂの大きさの1/3で、∠Ｂの大きさは∠Ｃの大きさの3/8になります。このとき、∠Ｂの大きさを求めてください。
△ABCの内角の和は180°になります。まずは、三角形の∠Cをχとして考えます。
そうすると、∠Bは∠Cの３／８ですから、
∠B＝（χ×3/8）＝3χ/8°
∠Aは、∠Bの1/3ですから
∠A＝3χ/8×1/3＝χ/3°
３つの角の合計は。１８０°になりますから。
180°＝∠A＋∠B＋∠C
＝（3χ/24°）＋（3χ/8°）＋（χ°）
＝3χ/24°＋9χ/24°＋24χ/24°
＝36χ/24°
＝3χ/2°
χ＝2/3×180°
＝120°
∠Ｃ＝χ＝120°
∠Ｂ＝3χ/8° にχ＝120を代入します。
3×120÷8＝∠Ｂ
360÷8＝45
∠Ｂ＝45°
答え ∠Ｂ＝45°
（２）∠Ａ＝40°の△ＡＢＣがあります。∠Ｂの大きさがどのような範囲のとき、△ＡＢＣが鋭角三角形となるのか答えてください。
鋭角三角形は、すべての角度が90°までになりますから、
∠Ａが40°となると、残りの２つの角の角度の合計は
180°−40°＝140°
∠Ｂ＋∠Ｃ＝140°
∠Ｂが89°のとき、∠Ｃは51°になります。
同じように、∠Ｃが、89°のとき、∠Ｂは51°になります。
求めているのは、∠Ｂの範囲ですから、
50°＜∠Ｂ＜90°
になります。
答え 50°＜∠Ｂ＜90°
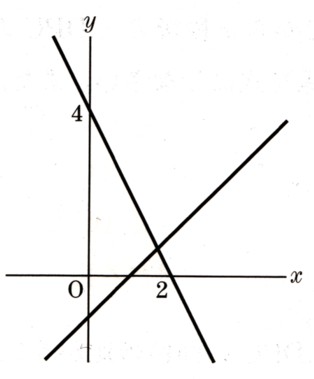
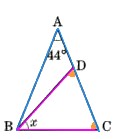
（３）図
において、ＡＢ＝ＡＣ，ＢＣ＝ＢＤとすると、∠Ａ＝44°のとき、∠χの大きさを求めてください。
において、ＡＢ＝ＡＣ，ＢＣ＝ＢＤとすると、∠Ａ＝44°のとき、∠χの大きさを求めてください。
コメント