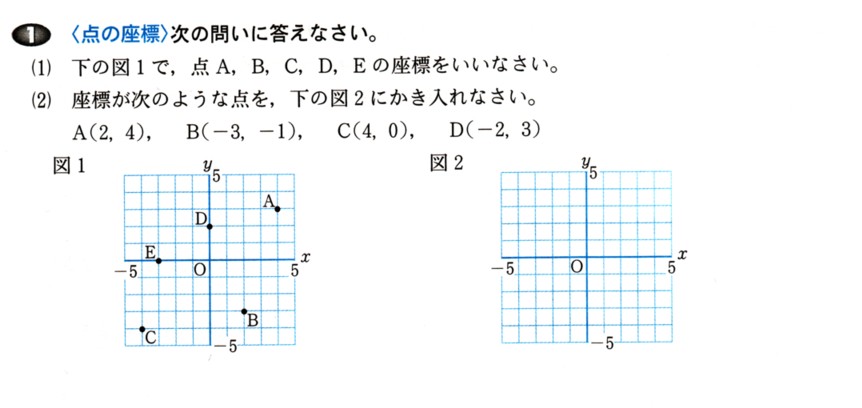
中学2年数学 1次関数 2元1次方程式とグラフ 確認問題5・解答
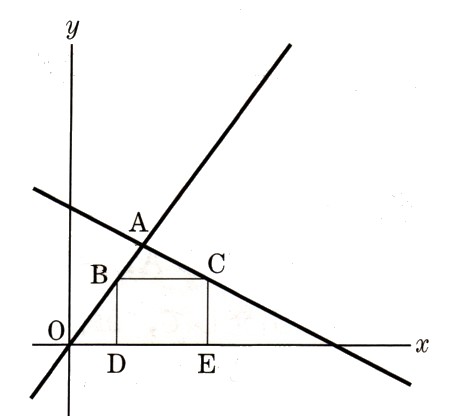
5、図 のように、関数 y=2χ、y=aχ+6 のグラフがあります。
のように、関数 y=2χ、y=aχ+6 のグラフがあります。
この2つのグラフは交わっていて、その交点をAとします。また、関数 y=2χのグラフ上に2点O,Aの間に点Bをとり、関数 y=aχ+6のグラフ上に点Cをとります。2点B,Cからχ軸に引いた垂線とχ軸との交点をそれぞれD,Eとします。ただし、a<0とします。
これについて、次の問いに答えてください。
(1)直線OAが点(4、b)を通るとき、bの値を求めてください。
原点Oを通っていますから、切片の無い式は y=2χ になります。
直線OAの式 y=2χ に座標(4、b)を代入します。
b=2×4
b=8
点Aの座標は(4,6)とわかりました。
答え b=8
(2)a=−2のとき、点Aの座標を求めてください。
関数 y=2χ は、わかっていますから、点Aの座標を求めるために
2つの直線の連立方程式をつくります、その値が2直線の交点Aになります。
交点A=A座標 になります。
aがあるのは、関数 y=aχ+6 になります。
a=−2ですから、y=aχ+6 の式に a=−2 を代入します。
y=(−2)χ+6
連立方程式をつくります。
y=(−2)χ+6
{
y=2χ
y=(−2)χ+6 に y=2χ を代入します。
(2χ)=−2χ+6
2χ+2χ=6
4χ=6
χ=6/4
χ=3/2
y=2χ に χ=3/2 を代入します。
y=2(3/2)
y=3
点Aの座標がわかりました。
答え χ=3/2 、y=3
(3)点Dの座標が(2,0)であり、四角形BDECが正方形になるとき、aの値を求めてください。
Dの座標はわかっていますから、関数 y=2χ の点Bのχの座標(2、y)はわかります。
y=2χ の式のχに2を代入すれば、点Bの座標がわかります。
y=2(2)
y=4
点Bの座標がわかれば正方形になるのだから、1辺の長さは4とわかります。図
点B(2、4)、点C(6、4),点D(2、0),点E(6、0)となります。
これで、関数 y=aχ+6 の直線の座標点C(6、4)がわかりました。
y=aχ+6 の式に,(6、4)を代入します。
(4)=a(6)+6
4=6a+6
6a+6=4
6a=4−6
6a=−2
a=−1/3
y=aχ+6 のaの値がわかりました。
答え a=−1/3







コメント