中学2年数学　連立方程式　2まとめテスト６(1)・解答

中学2年数学　連立方程式　2まとめテスト６(1)・解答

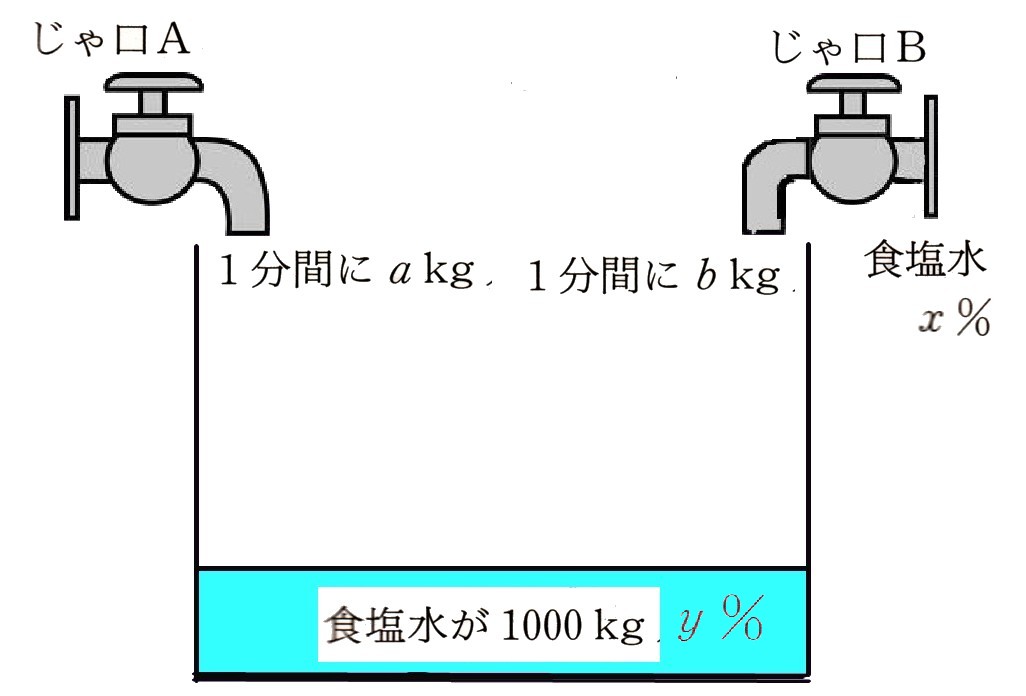
6、食塩水が1000?入った水槽と、Ａ，Ｂの2つの蛇口があります。蛇口Ａは水を1分間にａ?入れることができます。

　　蛇口Ｂはχ％の食塩水を1分間にｂ?入れることができます。

　　次の操作1～3を順に行ったときに、次の問いに答えてください。

（操作1）

　　蛇口Ａを2分間、蛇口Ｂを4分間、それぞれ開けた後に、水槽内の食塩水を測定すると、重さは2000?となり、濃度は最初よりもｍ％だけ高くなりました。

（操作2）

　　（操作1）の状態から、蛇口Ａを14分間、蛇口Ｂを3分間それぞれ開けた後に水槽内の食塩水を測定すると、重さは4000kgとなり、その濃度は（操作1）を行う前の最初の濃度よりもｍ％だけ低くなりました。

（操作3）

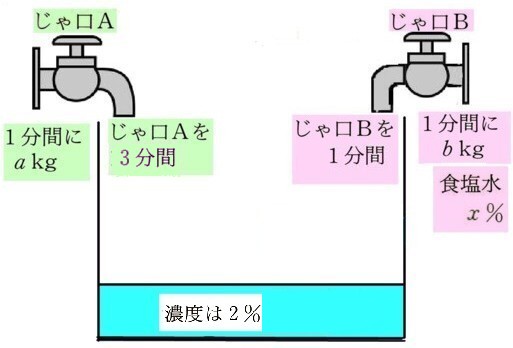
　　水槽の食塩水をすべて抜き、蛇口Ａを3分間、蛇口Ｂを1分間それぞれ開けました。後に水槽内の食塩水を測定すると、その濃度は２％でした。

（１）ａの値を求めてください。

　　　最初の濃度がわかりませんから、食塩水の量で考えていきます。

　　　食塩水の量は、

　(操作1)で、　（1000）?＋（蛇口Ａを2分間、開けた水量）＋（蛇口Ｂを4分間、開けた食塩水の量）＝（水槽の水量）?

　　　水量は＝(毎分の水量)×(時間)

　　　（蛇口Ａを2分間、開けた水量）＝ａ?×2(分間)

　　　　　　　　　　　　            　　　　　＝2ａ(?)

　　　（蛇口Ｂを4分間、開けた食塩水の量）＝ｂ?×4(分間)

　　　　　　　　　　　　　　　　　　　　＝4ｂ(?)

　　　（水槽の水量）＝2000kg

　　　　　1000＋2a＋4ｂ＝2000

　　　　次に、(操作2)でも同じように、　

　　　　（2000）?＋（蛇口Ａを14分間、開けた水量）＋（蛇口Ｂを3分間、開けた食塩水の量）＝（水槽の水量）?

　　　　　（蛇口Ａを14分間、開けた水量）＝ａ?×14(分間)

　　　　　　　　　　　　　　　　　　          　　＝14ａ(?)

　　　　　（蛇口Ｂを3分間、開けた食塩水の量）＝ｂ?×3

　　　　　　　　　　　　　　　　　　　　              　　 ＝3ｂ(?)

           （水槽の水量）＝4000kg

         2000＋14ａ＋3ｂ＝4000

       連立方程式を作ります。

　　　　1000＋2a＋4ｂ＝2000
　　｛
　　　　2000＋14ａ＋3ｂ＝4000

　　　　2a＋4ｂ＝2000−1000
　　｛
　　　　14ａ＋3ｂ＝4000−2000

　　　　2a＋4ｂ＝1000
　　｛
　　　　14ａ＋3ｂ＝2000

　　　　14ａ＋28ｂ＝7000
　　｛
　　　　14ａ＋3ｂ＝2000

　　　 14ａ＋28ｂ＝7000
　　−)14ａ＋3ｂ＝2000
                25ｂ＝5000

  ｂ＝200

    2a＋4ｂ＝1000　に　ｂ＝200　を代入します。

　　2a＋4（200）＝1000

　　2a＋800＝1000

　　2a＝1000−800

　　2a＝200

　　a＝100　

　　　答え　a＝100　、ｂ＝200

  蛇口
Ａの毎分の水量　100ｋｇ

　蛇口Ｂの毎分の水量　200?