中学２年数学 図形の調べ方 図形の合同 練習問題4・解答
４、合同な図形の性質
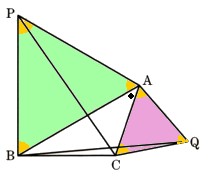
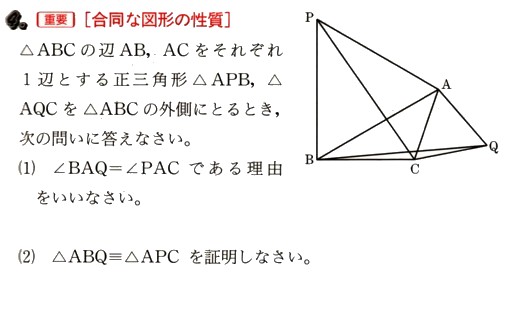
△ABCの辺AB,ACをそれぞれ1辺とする正三角形△APB、△AQCの外側にとるとき、次の問いに答えてください。
（１）∠BAQ＝∠PACである理由を述べてください。
△APBと△AQCは２つとも正三角形になります。 それにより、∠PAB＝60°
∠QAC＝60°
∠CABは、共通ですから。
∠BAQと∠PACは同じ角度であるといえます。
答え
△APBと△AQCは、正三角形ですから、
∠BAQ＝∠BAC+∠CAQ(正三角形の1つの内角)
＝∠BAC＋60°・・・①
∠PAC＝∠BAC＋∠BAP(正三角形の1つの内角)
＝∠BAC＋60°・・・②
①,②より、∠BAQ＝∠PAC
（２）△ABQ≡△APCを証明してください。
答え
△ABQと△APCにおいて、
(1)より、∠BAQ＝∠PAC・・・①
△APBは正三角形ですから
AB＝AP・・・②
△AQCは正三角形ですから
AQ＝AC・・・③
①～③より、
2辺とその間の角がそれぞれ等しくなるので、
△ABQ≡△APC
となります。
コメント