中学3年数学 図形と相似 2まとめテスト1・解答
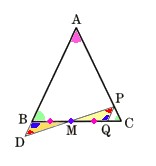
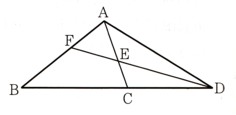
1、次の図 のように、△ABCの辺BCの延長上に、∠CBA=∠CADとなる点Dをとります。
のように、△ABCの辺BCの延長上に、∠CBA=∠CADとなる点Dをとります。
∠ADCの二等分線が辺AC,ABと交わる点をそれぞれE,Fとします。
このとき、次の問いに答えてください。
(1)△ADF∽△CDEであることを証明してください。

答え
[証明]
△ABDと△ADCで考えます。
仮定により、
∠ABD =∠CAD・・・?
∠BDA =∠ADC(共通)・・・?
?,?より
2組の角がそれぞれ等しく なります。
∴
となります。
次に、△ADFと△CDEで考えます。
仮定により
∠ADF =∠CDE・・・?
△ABD ∽△CADですから、
∠DAF=DCE ・・・?
?,?より
2組の角がそれぞれ等しく なりますから、
△ADF∽△CDE
となります。
(2)AE=3cm、EC=2cm、CD=6cmのとき、線分BCの長さを求めてください。
△CAD 
で考えます。
DE は∠Dの二等分線になりますから、
DA:DC=AE:EC
DC =6cm
AE =3cm
EC =2cm
ですから、
DA:6=3:2
DA×2=6×3
2 DA=18
DA =18/2=9
DAの長さは9cmとわかりました。
次に△ABDと△CAD は相似の関係ですから、
は相似の関係ですから、
△ABD∽△CAD
BD:AD=AD:CD
AD =9cm
CD =6cm
BD:9=9:6=3:2
BD:9=3:2
BD×2=9×3
2B







コメント