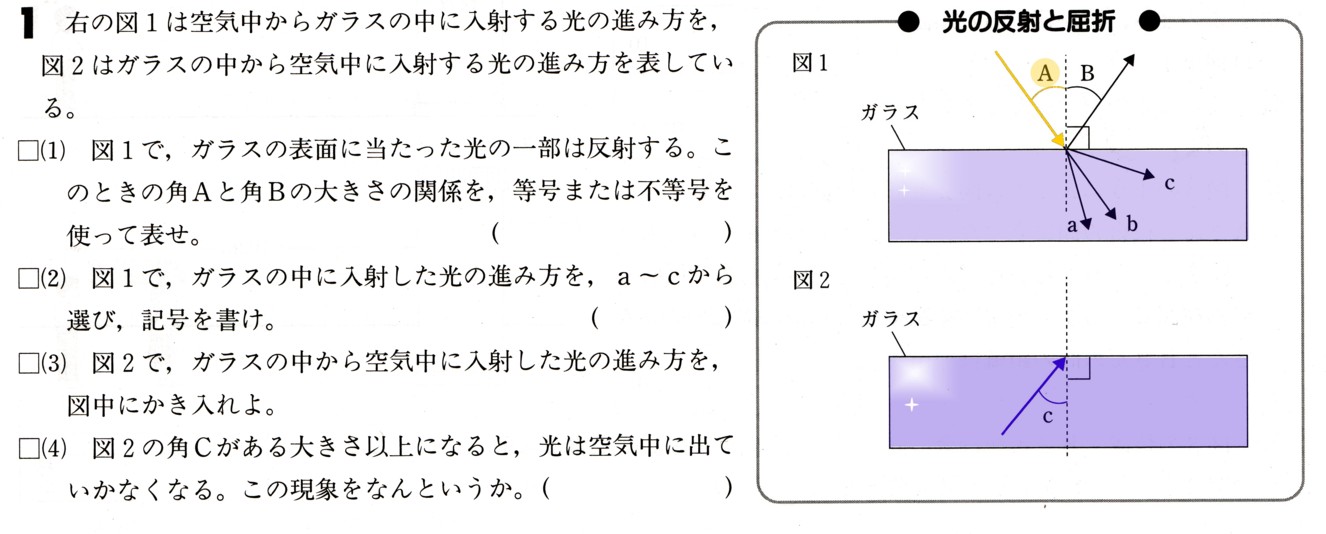
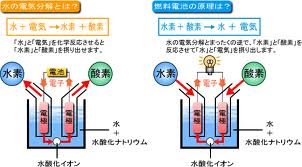
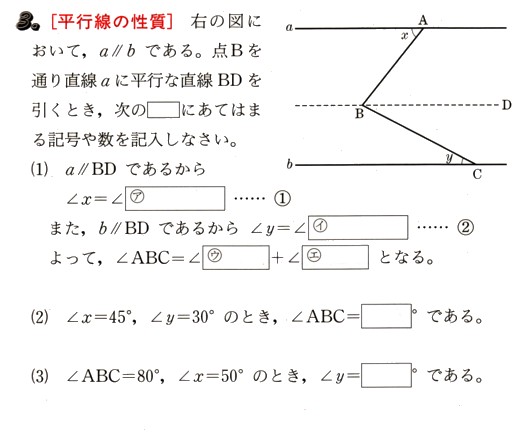
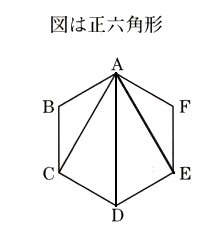
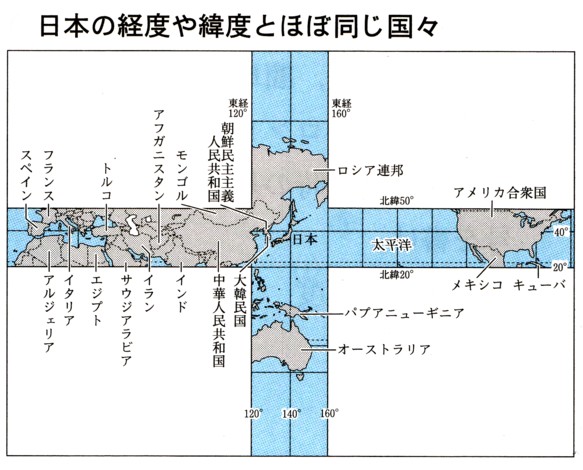
中学２年数学　１次関数　2元１次方程式とグラフ　確認問題３・解答

中学２年数学　１次関数　2元１次方程式とグラフ　確認問題３・解答

３、　χ/4 ＋ ｙ/3＝1・・・?
　　　
　　　2χ−ｙ＝0・・・?

　　　　　について、次の問いに答えてください。

（１）?のグラフと?のグラフの交点の座標を求めてください。

　　交点の座標は、連立方程式をつくってχ、ｙの解が2直線の交点の座標になります。

　　　χ/4 ＋ ｙ/3＝1
　｛
　　　2χ−ｙ＝0

　　　12(χ/4 ＋ ｙ/3)＝12×1

　　　3χ＋4ｙ＝12
　｛
　　　2χ−ｙ＝0

　　　3χ＋4ｙ＝12
　＋）8χ−4ｙ＝0
　　　11χ　　＝12

　　χ＝12/11

　　2χ−ｙ＝0　に　χ＝12/11　を代入します。

　　2（12/11）−ｙ＝0

　　24/11−ｙ＝0

　　−ｙ＝−24/11

　　ｙ＝24/11

　　2直線の交点の座標がわかりました。

　　(χ、ｙ)＝(12/11、24/11)

　　答え　χ＝12/11　、ｙ＝24/11 

（２）直線?の傾きと切片を求めてください。

　　傾きと切片を求めるためには

　　ｙ＝ａχ＋ｂ　の形にします。

　　ｙ＝ａ(傾き)＋(切片)

　　　　　　　　(ｙの増加量)　　
　　(傾き)＝―――――――
　　　　　　　　(χの増加量)　　　

　　　　(傾き)と(切片)がわかり(傾き)の符号が(＋)、(−)で傾きをかきます。

　　(＋)ならば右上がりになります。

　　(−)ならば右下がりになります。

　　?　χ/4 ＋ ｙ/3＝1

　　　 3χ＋4ｙ＝12　ということは(2)でわかりましたから、

　　　4ｙ＝−3χ＋12

　　　　ｙ＝−3/4χ＋3

　　(傾き)が3/4、(切片)が＋3とわかりました

　　　　　　　　　(ｙの増加量)　　 　　 3
　　(傾き)＝―――――――＝−――
　　　　　　　　　(χの増加量)　　  　4

　　(傾き)の符号が(−)ですから、右下がりになります。

　　答え　（傾き、−3/4　）、（切片、3）

(3) ?のグラフと、χ軸、ｙ軸との交点の座標をそれぞれ求めてください。

　　χ軸に接するということは、(χ、ｙ)＝(0、ｙ)　になり

　　ｙ軸に接するということは、(χ、ｙ)＝(χ、0)　になります。

　　?　χ/4 ＋ ｙ/3＝1

　　　 3χ＋4ｙ＝12　ということは(2)でわかりましたから、

　　　4ｙ＝−3χ＋12

　　　　ｙ＝−3/4χ＋3

　　ｙ＝−3/4χ＋3　に　(0、ｙ)　を代入します。

　　ｙ＝−3/4(0)＋3

　　ｙ＝(0)＋3

　　ｙ＝
3

　　ｙ＝−3/4χ＋3　に　(χ、0)　を代入します。
　　　
　　0＝−3/4χ＋3

　　−3/4χ＋3＝0

　　−3/4χ＝−3

　　χ＝−3×−4/3

　　χ＝4

　　　χ軸、ｙ軸の接する座標がわかりました。

　　答え　χ軸に接する座標は　(χ、ｙ)＝(4，0)、

　　　　 　ｙ軸に接する座標は　(χ、ｙ)＝(0，3)