中学3年数学 式の展開と因数分解 まとめテスト8・解答
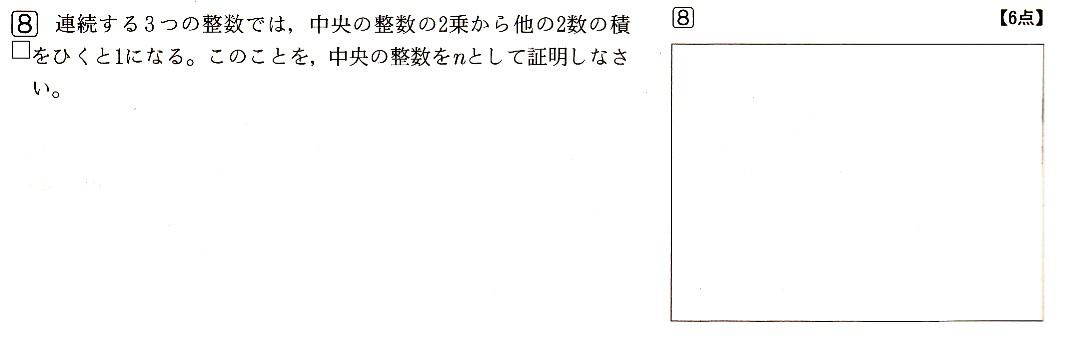
8、連続する3つの整数では,中央の整数の2乗から他の2数の積を引くと1になります。このことを、中央の整数をnとして証明してください。
答え
〈証明〉
連続する3つの整数とは、例1、2、3のような数のことをいいます。
真ん中の数をnとして考えます。
1つ前の数は(n−1)
1つ後の数は(n+1)
となり、(n−1)、n、(n+1)になります。
中央の整数とはnのことになりますから、他の2数の積を引くと1になるのですから、
n²ー{(n−1)×(n+1)}=1
となります。
乗法公式を利用します。
●(a+b)(aーb)=a²ーb²
{(n−1)×(n+1)}=n²ー1²
になりますから、
n²ー{(n−1)×(n+1)}=1
n²ー(n²ー1²)=1
n²ーn²+1²=1
1²=1
これにより、中央の整数の2乗から他の2数の積を引くと1になることがわかります。





コメント