中学2年数学　1次関数　　１まとめテスト5（２）・解答

中学2年数学　1次関数　　１まとめテスト5（２）・解答

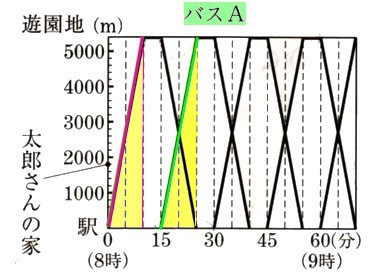
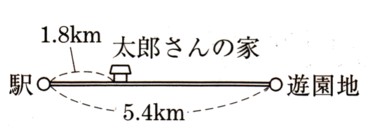
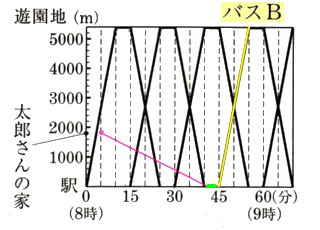
（３）駅を8時15分に出発するバスをバスAとして、太郎さんが家を出発してからの時間をχ分とします。次の問いに答えて下さい。

　?　バスAが駅から遊園地に向かうとき、駅からバスAまでの距離をｙmとして、ｙをχの式で表して下さい。

　　8時15分のグラフを見ます。

　　ｙ＝ａχ＋ｂ　　の式にします。

　　　　　　　　(ｙの増加量)　　　 5400
　　(傾き)＝―――――――＝――＝540
　　　　　　　　(χの増加量)　　   10

  (切片)をだすために、バスＡの出発の座標(25，5400)を代入し、(切片)を出します。

　　5400＝540×25＋ｂ

　　5400＝13500＋ｂ

　　13500＋ｂ＝5400

　　ｂ＝5400−13500

　　ｂ＝−8100

　　(切片)＝−8100　とわかりました。

　　　ｙ＝ａχ＋ｂ

　　　　ｙ＝(傾き)χ＋(切片)

　　　答え　　ｙ＝540χ−8100 

　?　バスＡが遊園地から駅に戻るとき、太郎さんと出会う時間は何時何分になりますか？求めて下さい。

　　バスＡのグラフを考えます。

　　(傾き)は、行きの(傾き)と同じですが符号は、右上がりと右下がりですから、帰りの傾きは(−)になります。

　　(傾き)＝−540

　　　ｙ＝ａχ＋ｂ　の式にあてはめ、座標(40，0)を代入します。

　　　0＝−540×40＋ｂ

　　　0＝−21600＋ｂ

　　　ｂ＝21600

　　　　ｙ＝−540χ＋21600

　　とわかりました。

　　　バスＡと太郎さんが出会うということはバスＡの式と太郎さんの式の交点になります。

　　　2つの式のχ値が太郎さんとバスＡの出会う時間になります。

　　　バスＡの式はわかりました、太郎さんの式は(切片)1800  (傾き)（5400−1800/60）＝60

　　　バスＡの式　　    ｙ＝−540χ＋21600

　　　太郎さんの式　　ｙ＝60χ+1800

　　　　ｙ＝−540χ＋21600
　　｛
　　　　ｙ＝60χ+1800

　　　　　540χ＋ｙ＝21600
　　｛
　　　　−60χ+ｙ＝1800

　　　　　540χ＋ｙ＝21600
　　−)  −60χ+ｙ＝1800
          600χ   ＝19800

  χ＝33

　　　答え　8時33分