中学2年数学 確率 場合の数 確認問題5・解答
5、男子3人、女子2人からなる5人グループがあります。次の問いに答えてください。
男子をA、B、Cとし、女子をA’,B’として考えます。
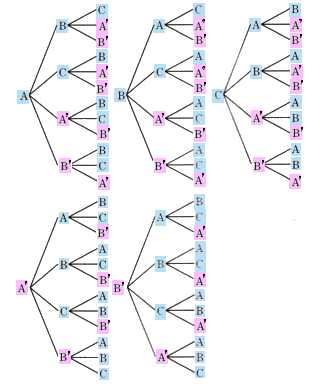
(1)5人の中から3人を選んで1列に並べる並べ方は何通りありますか?

(先頭)は、5人全員並ぶことができます。
(真ん中)は、先頭に並んだ一人以外の4人が並ぶことができます。
(最後)は、先頭と真ん中に並んだ二人以外の3人が並ぶことができます。
(先頭の場合の数)×(真ん中の場合の数)×(最後の場合の数)=(通り)
5×4×3=60(通り)
答え 60(通り)
(2)5人の中から2人の委員を選ぶ選び方は何通りありますか?

一人目を選ぶ場合の数は、5人全員になります。
二人目の委員を選ぶときは1人が決まっているので、4人になります。
ただし、2人の委員は前後しても同じ人物なので出た答えを半分にしないといけません。
(一人目の場合の数)×(二人目の場合の数)÷2=(通り)
5(人)×4(人)÷2=10(通り)
答え 10(通り)
(3)5人の中から,男女1人ずつの委員を選ぶ選び方は何通りありますか?
男子の場合は3人いますから3通りになり、
女子の場合は2人いますから2通りになります。
(男子の場合の数)×(女子の場合の数)=(通り)
3(通り)×2(通り)=6(通り)
答え 6(通り)







コメント