中学３年数学 式の展開と因数分解 式の計算の利用 ２確認問題１・解答
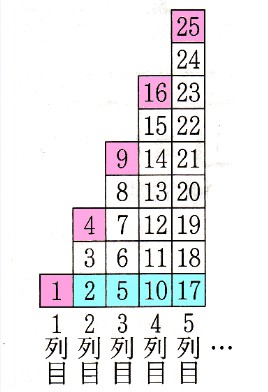
１、連続する自然数が書かれているカードがあります。このカードを１列目から順番に、１枚、３枚、５枚、７枚、９枚・・・と、図
のように規則正しく並べていきます。
のように規則正しく並べていきます。 花子さんと太郎さんは、気づいたことを次のように発表しました。
次の問いに答えてください。
花子さん：１列目から順に１枚，３枚、５枚、７枚、９枚・・・のカードが並んでいますから、ｎ列目には（２ｎー１）枚のカードが並びます。
太郎さん：各列の一番上の数は、１列目から順に１，４，９，１６，２５・・・になっていますから、ｎ列目の一番上の数はｎ²で表すことができます。
（１）１つの列に１５枚のカードが並ぶのは何列目になりますか？
花子さんから、ｎ列目には（２ｎー１）枚のカードが並びますから。
１５＝（２ｎー１） を利用します。
２ｎー１＝１５
２ｎ＝１５＋１
ｎ＝１６／２
ｎ＝８
ｎは何列目かを表しますから、
１５枚のカードが並ぶのは８列目になります。
答え ８列目
（２）１０列目の下から２番目のカードの数を答えてください。
太郎さんの考えから、
１列目は、１²＝１が一番上の数
２列目は、２²＝４が一番上の数
３列目は、３²＝９が一番上の数
・
・
・
９列目は、９²＝８１が一番上の数
１０列目は、１０²＝１００が一番上の数
ということは、１０列目の数は８２～１００になります。
下から２番目ですから８３となります。
答え ８３
（３）花子さんの考えの正しいことを，太郎さんの考えを使って証明してください。
太郎さんの式でｎ列目のカードの枚数を考えます。
図で考えてみましょう。
ｎ列目の１番上の数から１つ前の一番上の数を引けばｎ列のカードの枚数がわかります。
例：５列目の一番上の数・・・２５
４列目の一番上の数・・・１６
２５−１６＝９（枚）
となります。
花子さんの式は（２ｎー１）
５列目ですから（２×５ー１）＝（１０ー１）＝９（枚）
になります。
ｎ列目の一番上の数はｎ²
１列目は、１²＝１が一番上の数
２列目は、２²＝４が一番上の数
３列目は、３²＝９が一番上の数
４列目は、４²＝１６が一番上の数
・
・
・
ｎは何列目かを表しますから、
1つ前の列（ｎー１）の一番上の数は（ｎー１）²と表すことができます。
２列目の１つ前は（２ー１）²＝１²＝１
３列目の１つ前は（３−１）²＝２²＝４
４列目の１つ前は（４−１）²＝３²＝９
５列目の１つ前は（５−１）²＝４²＝１６
ｎ列目の１つ前のカードの一番上の数は、（ｎー１）²になります。
ですから、
（ｎ列目の一番上のカードの数）ー（ｎ列目の１つ前の列の一番上の数）＝（ｎ列目のカードの枚数）
ｎ²ー（ｎー１）²
乗法式を利用します。
●（ａ＋ｂ）²＝ａ²ー２ａｂ＋ｂ²
〔答え〕
ｎ²ー（ｎー１）²
＝ｎ²ーｎ²ー２×ｎ×（ー１）＋（ー１）²
＝ｎ²ーｎ²＋２ｎ＋１
＝２ｎ＋１
花子さんの考えた式は（２ｎ＋１）ですから、花子さんの考えは正しいということがわかります。
コメント