中学３年数学　三平方の定理の利用　２確認問題３・解答

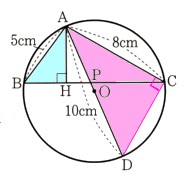
３、図のように、△ＡＢＣにおいて、頂点Ａから辺ＢＣに引いた垂線と辺ＢＣとの交点をＨ
とします。

また、頂点Ａ，Ｂ，Ｃを通る円の中心をＯとし、直線ＡＯと辺ＢＣの交点をＰ、円との交点をＤとします。

ＡＢ＝５?，ＡＣ＝８?，ＡＤ＝１０?のとき、次の問いに答えてください。

（１）△ＡＢＨ∽△ＡＤＣを証明してください。

答え

[証明]

△ＡＢＨと△ＡＤＣで

∠ＡＨＢ＝∠ＡＣＤ＝９０゜・・・?

ＡＤは中点Ｏを通る直線になります、∠ＡＣＤは弦ＡＤの円周角になりますから１８０／２゜＝９０゜

次に弦ＡＣで∠ＡＢＣ＝∠ＡＤＣ（円周角が同じ）・・・?

?，?より

２組の角がそれぞれ等しく なりますから

△ＡＢＨ∽△ＡＤＣ

になります。

（２）線分ＡＨの長さを求めてください。

（１）により

△ＡＢＨ∽△ＡＤＣ とわかりましたから、

ＡＤ：ＡＢ＝ＡＣ：ＡＨ

ＡＤ＝１０ｃｍ

ＡＢ＝５?

ＡＣ＝８ｃｍ

ＡＨ＝χ? として考えます。

１０：５＝８：χ

１０ ×χ＝５×８

１０ χ＝４０

χ ＝４

χ ＝ＡＨ＝４ｃｍ

答え　４ｃｍ

（３）ＰＤ／ＡＰの値を求めてください。

（２）により、ＡＨ＝4ｃｍ

ＡＣ＝８? ですから

△ＡＥＣは正三角形ということがわかります。

斜辺を8ｃｍとする△ＡＨＣは底辺をＡＨ＝４?とすると

∠ＨＡＣ ＝６０゜ということがわかります。

これにより、∠ＡＣＥ＝６０゜＝∠ＥＡＣになります。

∠ＡＣＤ＝90゜ですから、∠ＡＣＨ＝∠ＡＣＤ−∠ＥＡＣ

∠ＡＣＨ＝９０゜−６０゜＝３０゜

次に点Ｄから辺ＰＣに垂線を引きます。ＰＣと交わる点をＩとして考えます。

∠ＣＩＤ＝９０゜

∠ＩＣＤ＝６０゜

△ＣＡＨと△ＤＣＩで考えます。

∠ＡＨＣ＝∠ＣＩＤ＝９０゜・・・?

∠ＡＣＨ＝∠ＡＣＤ−∠ＰＣＤ

＝９０゜−６０゜

＝３０゜

これにより、∠ＣＡＨ＝１８０−（９０゜＋３０゜）

∠ＣＡＨ＝60゜

∠ＣＡＨ＝∠ＤＣＩ＝６０゜・・・?

?，?より

△ＣＡＨ∽△ＤＣＩ

になります。

ＣＤの長さは△ＡＣＤで考えます。

三平方の定理で考えます。

（底辺）²＋（高さ）²＝（斜辺）²

ＣＤ²＋ＡＣ²＝ＡＤ²

ＣＤ＝χとして考えます。

ＡＣ＝８?

ＡＤ＝10cm

χ²＋８²＝１０²

χ²＋６４＝１００

χ²＝１００−６４

χ²＝３６

χ＝６（χは＋になります。）

ＣＤ＝6?・・・?

△ＤＣＩの斜辺の長さがわかりました。

△ＣＡＨ∽△ＤＣＩ ですから、

ＡＣ：ＡＨ＝ＣＤ：ＣＩ

ＡＣ＝8?

ＡＨ＝4ｃｍ（２）より

ＣＤ＝６? ?より

ＣＩ＝χ?として考えます。

８：４＝６：χ

8×χ＝４×６

8χ＝２４

χ＝24／8＝３cm・・・?

ＤＩの長さを求めるために三平方の定理を利用します。

（底辺）²＋（高さ）²＝（斜辺）²

底辺＝ＣＩ＝3ｃｍ（?より）

高さ＝ＤＩ＝χとします。

斜辺＝ＣＤ＝６?（?より）

（3ｃｍ）²＋（χ）²＝（６?）²

９＋χ²＝３６

χ²＝３６−９

χ²＝２７（χは＋になります。）

χ＝√２７＝3√３?・・・?

次に、△ＡＨＰと△ＤＩＰで考えます。

∠ＡＨＰ＝∠ＤＩＰ＝９０゜・・・?

∠ＡＰＨ＝∠ＤＰＩ（対頂角）・・・?

?．?より

2組の角がそれぞれ等しくなりますから

△ＡＨＰ∽△ＤＩＰ

になります。

これにより、ＡＨ：ＤＩ

ＡＨ＝4ｃｍ（２）より

ＤＩ＝3√３? ?より

ＡＨ：ＤＩ＝４：3√３

ＡＨ：ＤＩ＝ＡＰ：ＰＤ

ＡＰ：ＰＤ＝４：3√３

これにより、ＰＤ／ＡＰの値は

3√３／４になります。

答え　3√３／４