中学1年数学　立体の表面積と体積　確認問題4　解答・解説

中学1年数学　立体の表面積と体積　確認問題4　解答・解説

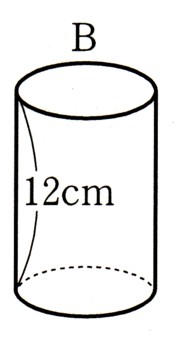
　　図のように、底面の半径が等しい円錐Aと円柱Bがあります。円錐Aの高さが6cm、

　円柱Bの高さが12cmのとき、円柱Bの体積は円錐Aの体積の何倍になりますか？

　　まずは、円柱と、円錐の体積を求める式で考えていきましょう。

　　円柱の体積を求める式は、

　　(円柱の体積)＝πγ²×高さ

　　円錐の体積を求める式は、

　　(円錐の体積)＝1/3πγ²×高さ

　　　になります。

　　この式からわかるように、

　　円錐の体積は、同じ底面積であれば円柱の1/3になります。

　　　今回は、底面の面積は円柱も円錐も同じですから1/3になります。ただし、高さが

　　円柱は、円錐の2倍になってます。

　　　少し円柱の形を変えてみましょう。

　　Bの円柱を半分に分けます。そうすると、2つの高さが同じの円柱が2つできます。

　　この円柱は、底面の面積は、円錐の面積と同じですから、

　　(高さ6?の円柱)＋(高さ6?の円柱)＝(高さ12?の円柱)

　　底面積は、円柱も円錐もすべて同じ。

　　(高さ6?の円柱)は(高さ6?の円錐)の3倍になります。

　　　　　　　　　　　　　　　(高さ6?の円柱)＝3×(高さ6?の円錐)
　　(高さ12?の円柱){
　　　　　　　　　　　　　　　(高さ6?の円柱)＝3×(高さ6?の円錐)

　　になりますから、(高さ6?の円錐)の6倍になります。

　　　　答え　6倍