中学2年数学 式と計算 式の加法・減法 2確認問題5・解答
5、A=χ+3y,B=−χy−3z,C=y/2 +2z のとき、次の式をχ,y,z,を用いて表してください。
(1)A+B−C
まずは、それおぞれの数字を( )でくくります。
(χ+3y),(−χ+2y−3z),(y/2 +2z)
(χ+3y)+(−χ+2y−3z)−(y/2 +2z) ・・・・( )をはずします。
=χ+3y−χ+2y−3z−y/2 −2z ・・・→同類項をまとめます。
=χ−χ+3y+2y−y/2−3z −2z ・・・→分母をそろえます。
=6y/2+4y/2−y/2−5z
=9/2 y−5z
答え 9/2 y−5z
(2)A−B−C
(χ+3y),(−χ+2y−3z),(y/2 +2z)
(χ+3y)−(−χ+2y−3z)−(y/2 +2z) ・・・・( )をはずします。
=χ+3y+χ−2y+3z−y/2 −2z ・・・→同類項をまとめます。
=χ+χ−2y+3y−y/2+3z −2z ・・・→分母をそろえます。
=2χ−4y/2+6y/2−y/2+z
=2χ+y/2+z
答え 2χ+y/2+z
(3)A+2B−4C
(χ+3y),(−χ+2y−3z),(y/2 +2z)
(χ+3y)+2(−χ+2y−3z)−4(y/2 +2z) ・・・・( )をはずします。
=χ+3y−2χ+4y−6z−2y−8z ・・・→同類項をまとめます。
=χ−2χ+3y+4y−2y−6z−8z
=−χ+5y−14z
答え −χ+5y−14z
(4)−2A −2B +2C
(χ+3y),(−χ+2y−3z),(y/2 +2z)
−2(χ+3y)−2(−χ+2y−3z)+2(y/2 +2z) ・・・・( )をはずします。
=−2χ−6y+2χ−4y+6z+y+4z ・・・→同類項をまとめます。
=−2χ+2χ−6y−4y+y+6z+4z
=−9y+10z
答え −9y+10z
(5)3/2 A−2B −C/2
(χ+3y),(−χ+2y−3z),(y/2 +2z)
3/2(χ+3y)−2(−χ+2y−3z)−1/2(y/2 +2z) ・・・・( )をはずします。
=3/2 χ+9/2 y+2χ−4y+6z−y/4−z ・・・→同類項をまとめます。
=3/2 χ+2χ+9/2 y−4y−1/4 y+6z−z ・・・→分母をそろえます。
=3/2 χ+4/2 χ+18/4 y−16/4 y−1/4 y+6z−z
=7/2 χ+1/4 y+5z
答え 7/2 χ+1/4 y+5z




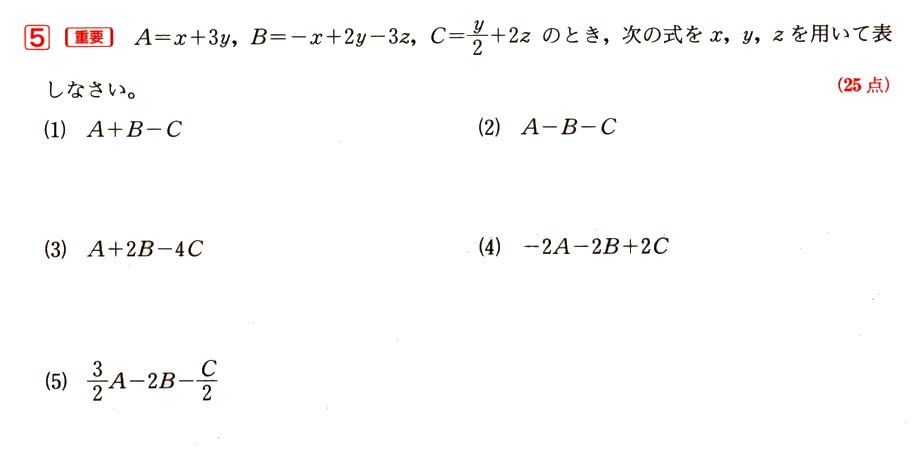
コメント