中学２年数学　図形の調べ方　２まとめテスト２・解答

中学２年数学　図形の調べ方　２まとめテスト２・解答

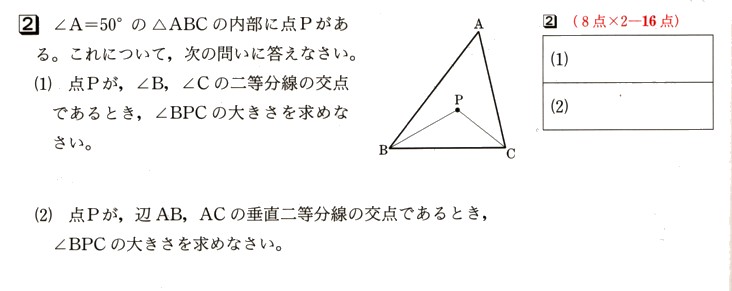
２、∠Ａ＝50°の△ＡＢＣの内部に点Ｐがあります。これについて、次の問いに答えてください。

（１）点Ｐが、∠Ｂ、∠Ｃの二等分線の交点であるとき、∠ＢＰＣの大きさを求めてください。

△ＡＢＣで考えます。

∠Ａが50°のとき、その他の２つの内角の和は、180−５０＝130°になります。

次に、△ＰＢＣについて考えます。

∠P＋（∠Ｂ×1／2）＋（∠Ｃ×1／2）＝180°

∠Ｂ＋∠Ｃ＝130°

二等分線ですから、半分になります。

130°÷2＝65°

∠Ｂ×1／2＋∠Ｃ×1／2＝65°になります。

∠Ｐ＋65°＝180°

∠Ｐ＝180−65

∠Ｐ＝115°

答え　115°

（２）点Ｐが、辺ＡＢ，ＡＣの垂直二等分線の交点であるとき、∠ＢＰＣの大きさを求めてください。

垂直二等分線ということは

辺ＡＢ、辺ＡＣの中点から垂線が引かれているということです。

よって、

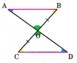
△ＡＤＰと△ＢＤＰにおいて

辺ＡＤ＝辺ＢＤ・・・①

∠ＢＤＰ＝∠ＡＤＰ・・・②

ＤＰ共通・・・③

２辺とその間の角がそれぞれ等しくなりますから

△ＡＤＰ≡△ＢＤＰ

合同な三角形の対応する角は等しくなりますから、

∠ＤＡＰ＝∠ＤＢＰ

次に、△ＡＰＥと△ＣＰＥにおいて

辺ＡＥ＝辺ＣＥ・・・①

∠ＡＥＰ＝∠ＣＥＰ・・・②

EP共通・・・③

２辺とその間の角がそれぞれ等しくなりますから

△ＡＰＥ ≡△ＣＰＥ

合同な三角形の対応する角は等しくなりますから、

∠ＥＡＰ＝∠ＥＣＰ

になります。

これにより、∠ＤＢＰ＋∠ＥＣＰ＝∠Ａ

になります。

四角形ＡＢＰＣの内角の和は360°になりますから

< /p>

∠Ａ＋（∠ＡＢＰ＋∠ＡＣＰ）＋∠ＢＰＣ＝360°

∠Ａ＝50°ですから、

50°＋50°＋∠ＢＰＣ＝360°

∠ＢＰＣ＝360°−100°

∠ＢＰＣ＝260°

360°から∠ＢＰＣの角度を引けば、∠ＢＰＣの角度がわかります。

360°−260°＝100°

＊∠ＢＰＣは、△ＡＢＰと△ＡＣＰの外角になります。

答え　∠ＢＰＣ＝100°