中学1年数学 立体の表面積と体積 確認問題6 解答・解説
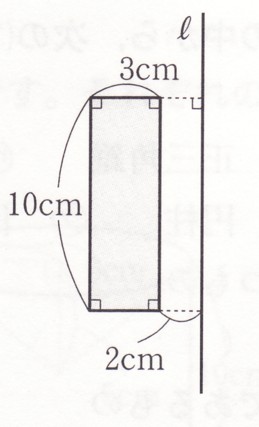
図の長方形や台形を、直線ℓを軸として1回転させてできる立体の体積と表面積を
求めてください。
このような図になります。
この図形の表面積を考えていきます
この表面積は、展開図で考えていきます。
展開図で考えると、表面積は
上底面、下底面、側面、内側面になります。
上底面と下底面は同じ面積になりますから
2×(底面積)+(側面積)+(内側面)になります。
内側面の面積は半径が2cmの円柱の側面の面積になります。
半径2cmの円柱の側面の形は長方形の形になります、この長方形の辺の長さは、1辺は高さ
10cm、もう1辺は半径2cmの円柱の円周になります。
この円周を求める式は
(円周)=2πγ
=2×(半径)×π
円周の半径は2cmですから
=2×2×π
=4πcm
内側面の面積は、4πcm×10cm=40π?²
次に、側面の面積を考えます。
側面の面積も、長方形になりますから1辺×1辺になります。
ひとつの1辺は高さですから、10cmになり、もう一つの辺の長さは、半径5cmの円の円周
の長さになります。
半径5cmの円の円周は、
(円周)=2πγ
=2×5×π
=10πcm
これで側面の2つの辺の長さがわかりました。
10cm×10πcm=100π?²
これで、側面の面積がわかりました。
次に、上底面の面積を求めます。
上底面の面積は、半径5cmの円から、半径2cmの円を除いた面積になります。
それではそれぞれの円の面積を考えていきましょう。
(円の面積)=πγ²
(半径5cmの円の面積)=(5cm)×(5cm)×π
=25π?²
(半径2cmの円の面積)=(2cm)×(2cm)×π
=4πcm²
(半径5cmの円の面積)−(半径2cmの円の面積)=(底面積)
25π?²−4πcm²=21πcm²
底面積は、上底と下底がありますから
2×21πcm²=42πcm²
これですべての表面積がわかりました。
表面積=2×(底面積)+(内側面積)+(外側面積)
=2×21πcm²+40π?²+100π?²
=42πcm²+40π?²+100π?²
=182π?²
次に、体積を考えていきましょう。
体積は、半径が5cm、高さが10cmの円柱から、半径が2cm、高さが10cmの円柱の体積を
除いた体積が、この筒状の立体の体積になります。
それでは、
円柱の体積を求める式から、2つの円柱の体積を求めます。
円柱の体積を求める式は
(円柱の体積)=Sh
=(底面積)×(高さ)
底面積は、円の面積になりますから。
=(円の面積)×(高さ)
(円の面積)=πγ²
=(半径)×(半径)×π
(円柱の体積)=(半径)×(半径)×π×(高さ)
それでは、半径5cmの円柱と、2cmの円柱を考えます。
?(円柱の体積)=5×5×π×10
=250πcm³
?(円柱の体積)=2×2×π×10
=40π?³
(筒状の立体の体積)=(?)−(?)
=250πcm³−40π?³
=210πcm³
答え 表面積 182π?² 、体積 210πcm³
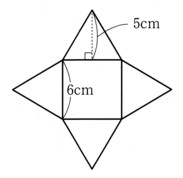
上底面の形がすり鉢状で、底面積は半径が4cmの円になります。
すり鉢状の部分は、三角錐のおうぎ形になります。
側面積は、1辺が6cm、もう1辺が半径4cmの円の周の長さになります。
それでは、わかりやすいように箇条書きでかいてみます。
?下底=円の面積
?上底=(三角錐の側面)=(おうぎ形)
?側面=長方形
?を考えていきましょう
下底=円の面積
になりますから、円の面積を考えます。
(円の面積)=πγ²
=(半径)×(半径)×π
(下底の半径4cmの円の面積)=(半径)×(半径)×π
=4×4×π
=16πcm²
?を考えていきましょう
上底=(三角錐の側面)=(おうぎ形)
(おうぎ形の面積)=πγ²×中心角/360
中心角の角度は、このままではわ












コメント