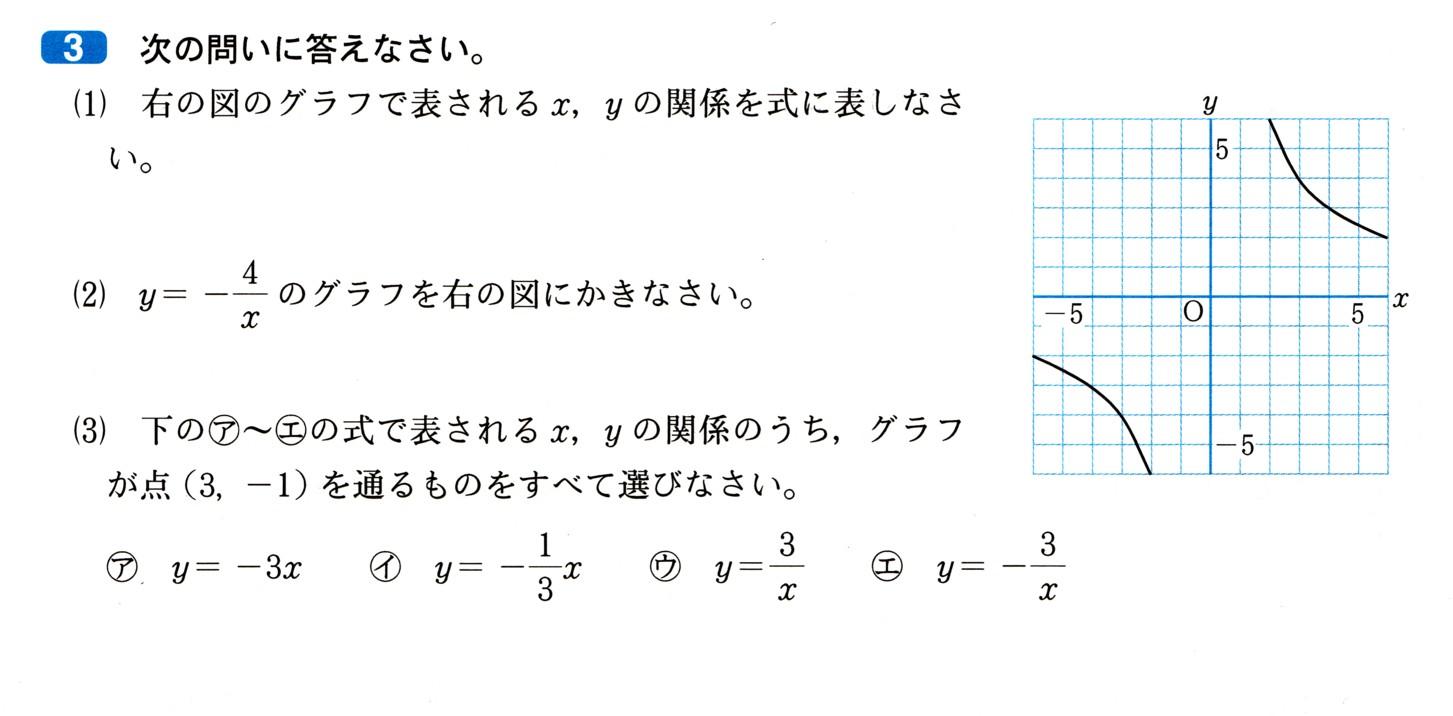
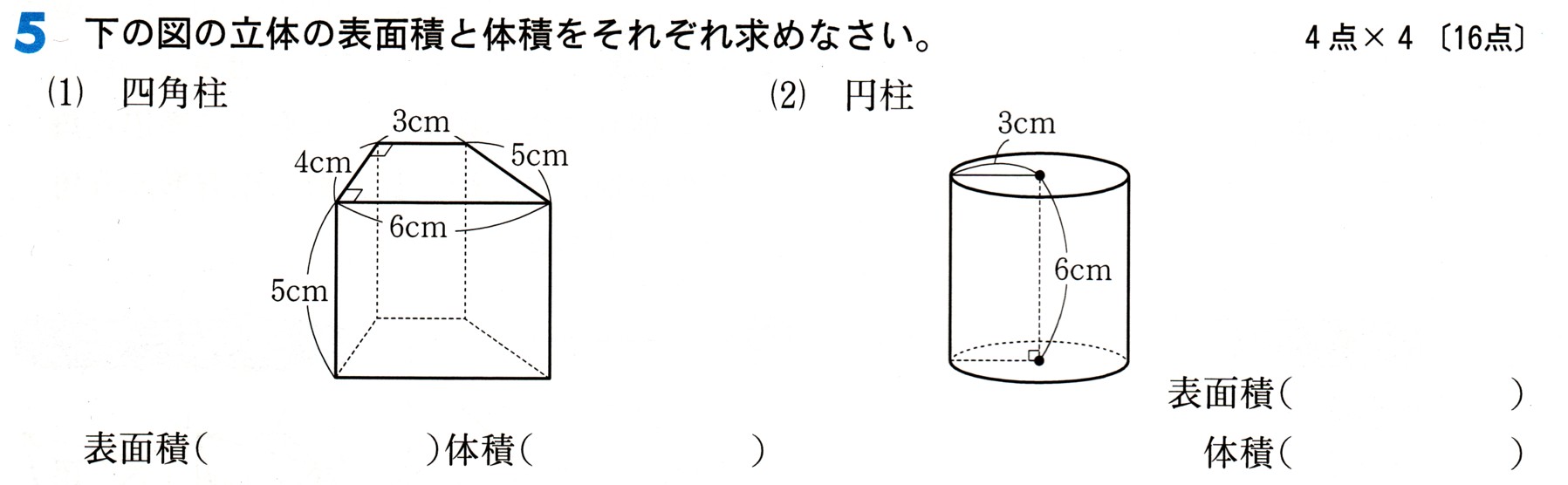
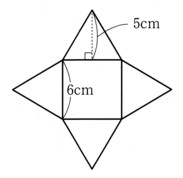
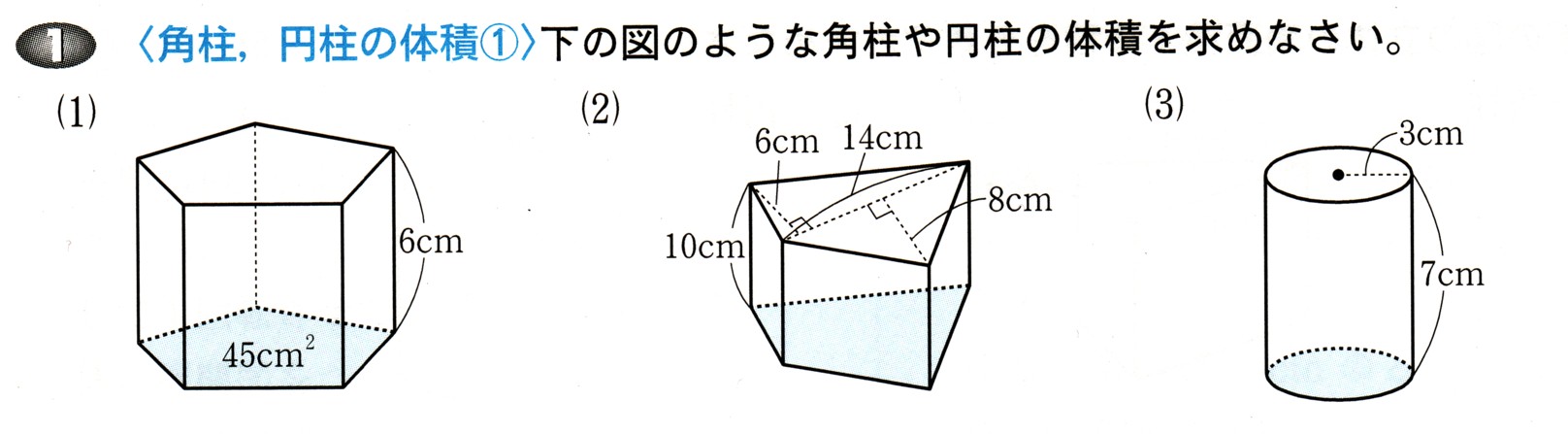
中学1年数学 立体の体積 練習問題1 解答・解説
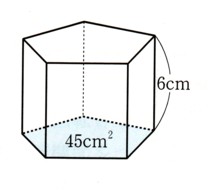
立体は、五角柱ということがわかります、
体積の求める式は、柱ですから、V=Sh
(体積)=(高さ)×(底面積)
今回は、底面積は45?²、高さは6cmとわかっていますから
(体積)=45×6
=270cm³
立方体の体積につける記号は(cm³)、(m³)・・・になり立方と読みます。
答え 270cm³
今回の図形は四角柱ですが、2つの三角形で、できていることがわかります。
それぞれの三角形の面積をだして、この四角柱の底面積をだしましょう。
? 底辺が6cm、高さが14cmの三角形の面積と、
? 底辺が14?、高さが8cmの三角形の面積になります。
三角形の面積=底辺×高さ×1/2
ですから、
?面積=6×14×1/2
=42cm²
?面積=14×8×1/2
=56?²
この四角柱の底面積は、?+? になりますから、
42cm²+56?²=98?²
底面積が98?²、高さは10cmですから
体積の求める式は、柱ですから、V=Sh
(体積)=(高さ)×(底面積)
この四角柱の体積は、
(体積)=10cm×98?²
=980cm³
単位を間違わないようにしてください。
(980立方cm)
答え 980cm³
今回の立体は、円柱です、
円柱の体積の求め方は。
V=Sh
(体積)=(底面積)×(高さ)
円柱の底面積は、円ですから、底面積はπγ²になります。
(体積)=(πγ²)×(高さ)
まずは底面積から、考えていきましょう
円の半径は(3cm)と、わかっていますから
円の面積は
円の面積=πγ²
=(半径)×(半径)×π
=3×3×π
=9πcm²
円柱の高さは、7?ですから
V=Sh
(体積)=(底面積)×(高さ)
=9πcm²×7?
=63πcm³
(63π立方cm)
*単位に気をつけてください。
答え 63πcm³


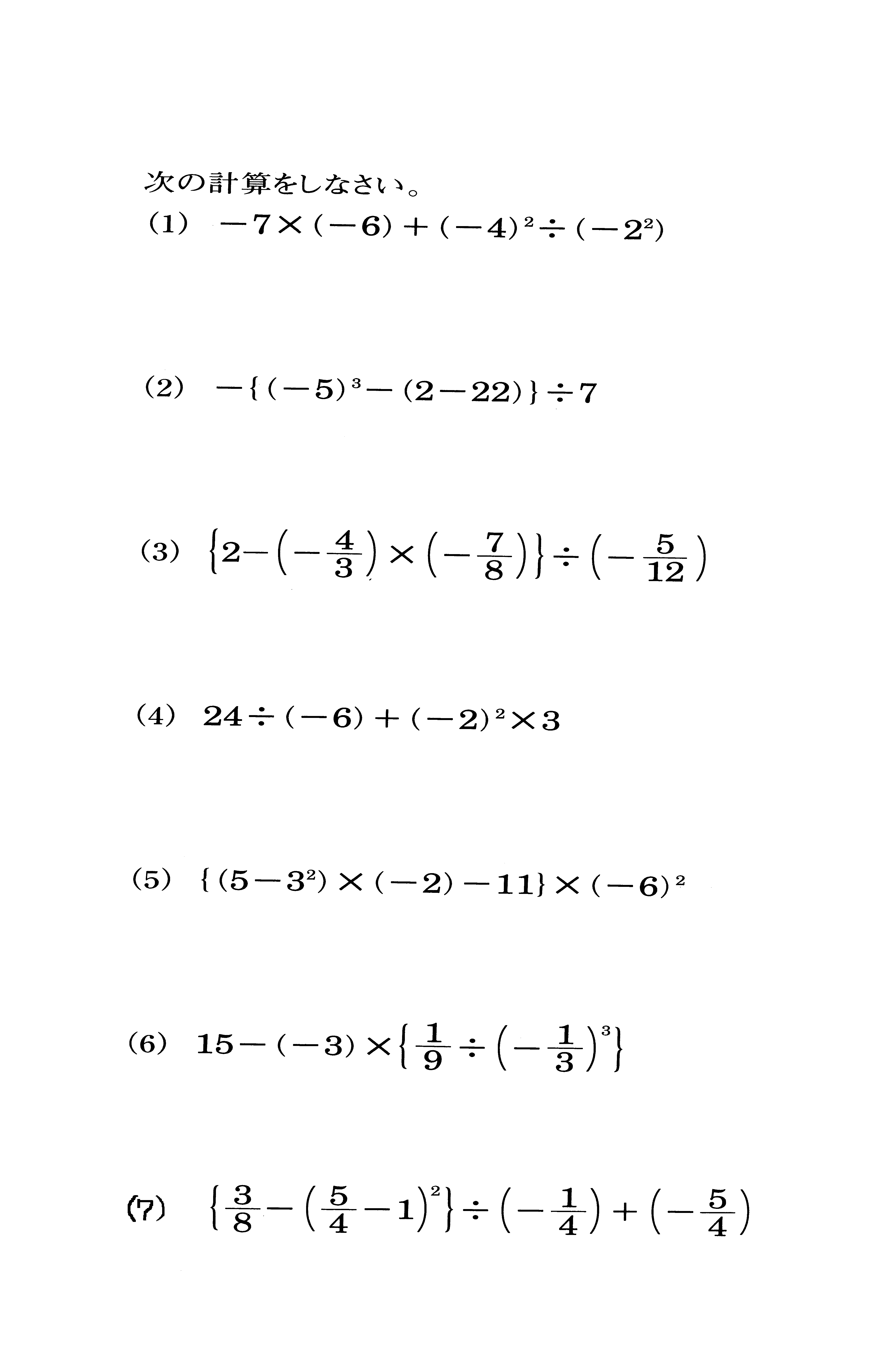











コメント