中学2年数学　円周角の定理　練習問題３・解答

中学2年数学　円周角の定理　練習問題３・解答

３、円周角の定理の利用

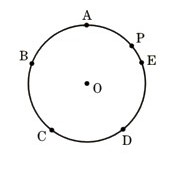
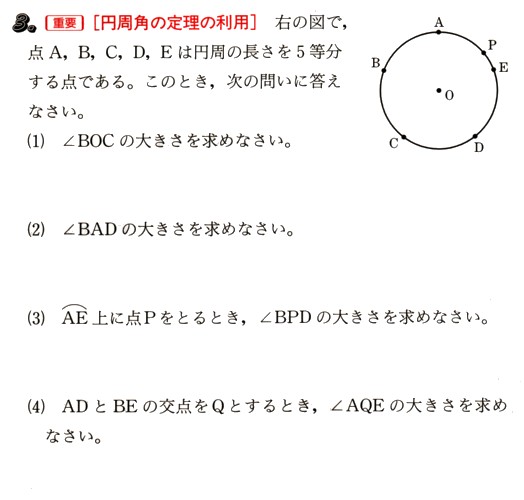
図で、点Ａ，Ｂ，Ｃ，Ｄ，Ｅは円周の長さを5等分にする点になります。このとき、次の問いに答えてください。

（１）∠ＢＯＣの大きさを求めてください。

△ＢＯＣで考えます。

∠ＢＯＣの中心角は、円の５分の１になりますから、

360°÷5＝72°になります。

∠ＢＯＣ＝72°

 

答え　∠ＢＯＣ＝72°

 

（２）∠ＢＡＤの大きさを求めてください。

弧ＡＢの中心角は、円周の５分の１ですから

∠ＡＯＢ＝72°

同じ弧の円周角は中心角の半分になりますから、

∠ＡＤＢ＝72°÷2

＝36°

になります。

△ＡＢＤはＤＡ＝ＤＢですから、

二等辺三角形になります。

頂角が∠ＡＤＢですから、36°になりますから、

底角が、180°ー36°＝144°

二等辺三角形は底角がそれぞれ等しくなりますから、

∠ＤＡＢ＝∠ＤＢＡ

になります。

ですから、∠ＢＡＤ＝144°÷2

＝72°

 

答え　∠ＢＡＤ＝72°

 

（３）Ａ⌒Ｅ上に点Ｐをとるとき、∠ＢＰＤの大きさを求めてください。

弧ＢＤで考えます。

弧ＢＤの中心角は、円の５分の２になりますから、

360°×２/５＝144°

∠ＢＰＤは、

弧ＢＤの円周角になりますから、

弧ＢＤの中心角の半分になります。

144°÷2＝72°

 

答え　∠ＢＰＤ＝72°

 

 

（４）ＡＤとＢＥの交点をＱとするとき、∠ＡＱＥの大きさを求めてください。

点Ａと、点Ｂをつなぐ補助線を引き

△ＡＱＢで考えます。

そうすると、

∠ＡＱＥは、△ＡＱＢの∠ＱＡＢと∠ＡＢＱの外角になります。

そのために、△ＡＢＱの２つの内角を考えていきます。

∠ＡＢＱは、弧ＡＥの円周角になります。

弧ＡＥの中心角は円の５分の１になりますから。

∠ＡＯＥ＝360×１／５

＝72°

円周角、∠ＡＢＥ＝72°×１／２

＝36°

∠ＡＢＥと∠ＡＢＱは同じ角ですから

∠ＡＢＱ＝36°・・・�

つぎに、∠ＱＡＢを考えます。

∠ＱＡＢは弧ＢＤの円周角になりますから、

弧ＢＤの中心角から考えます。

弧ＢＤの中心角は、円の５分の２になりますから、

∠ＢＯＤ＝360°×２／５

＝144°

弧ＢＤの円周角は中心角の半分になりますから、

∠ＢＡＤ＝144°×１／２

＝72°

∠ＢＡＤと∠ＢＡＱは同じ角ですから

∠ＢＡＱ＝72°・・・�

これで△ＡＢＱの２つの内角がわかりました。

この２つの内角の和は、外角∠ＡＱＥになります。

∠ＡＱＥ＝∠ＡＢＱ＋∠ＢＡＱ

＝36°＋72°

＝108°

 

答え　∠ＡＱＥ＝108°