中学２年数学 円周角の定理 平面図形 確認問題６・解答
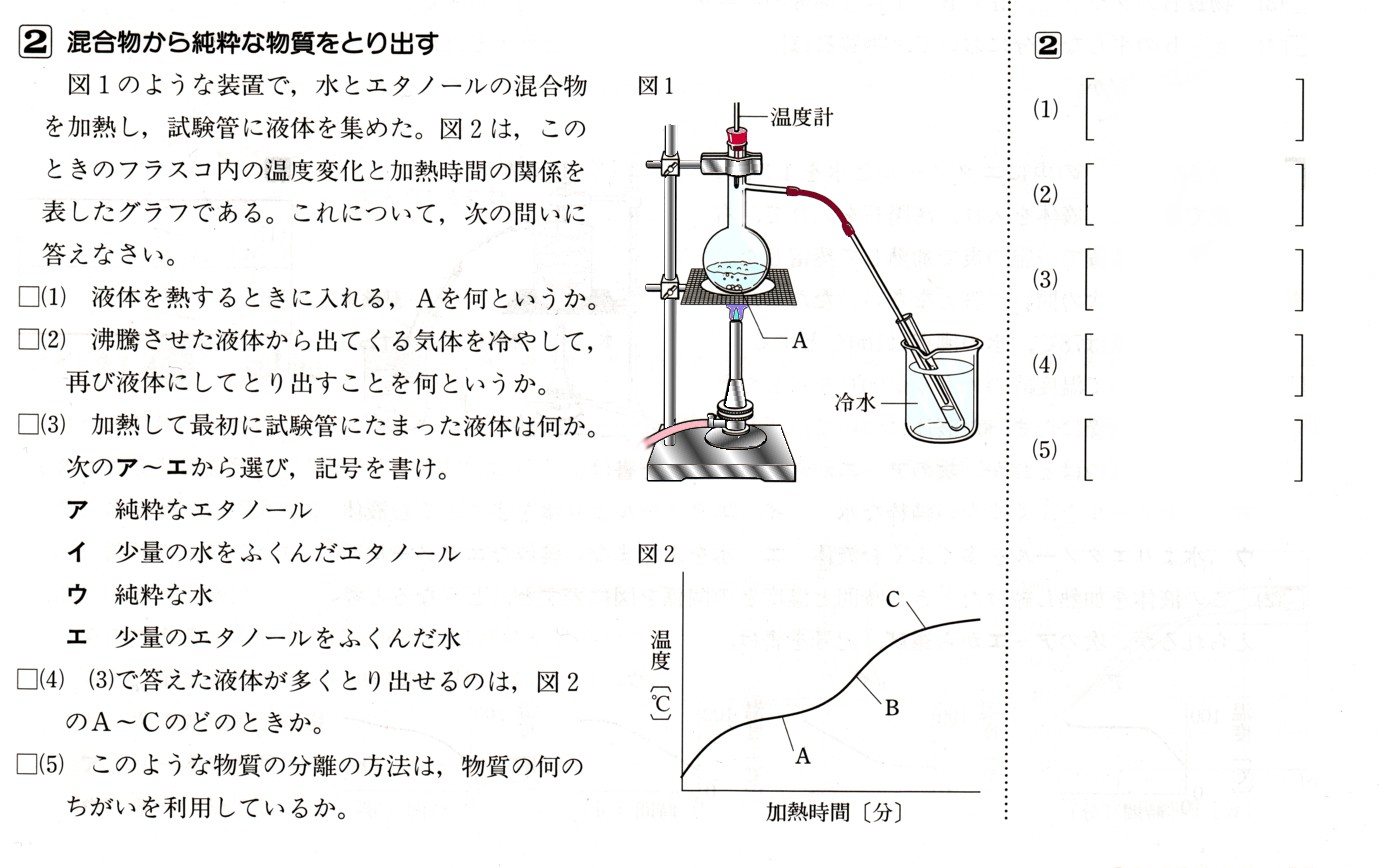
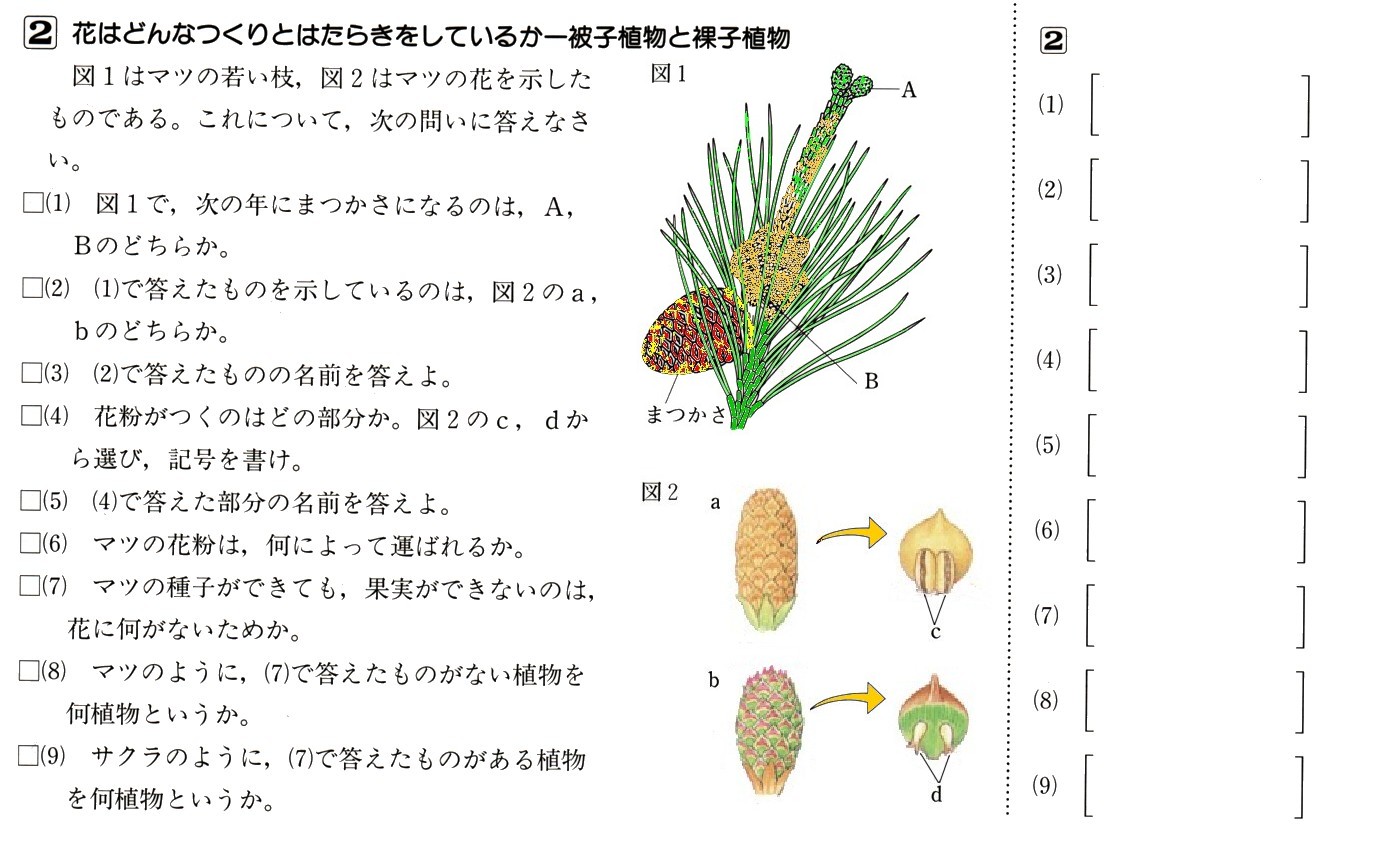
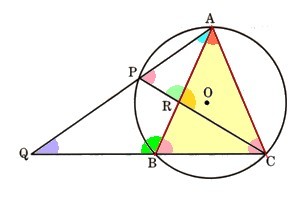
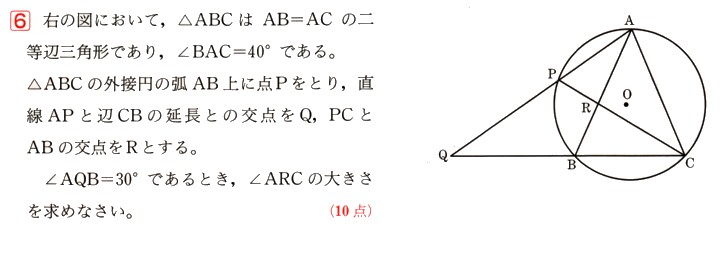
６、図
において、△ABCはAB＝ACの二等辺三角形であり、∠BAC＝40°になります。△ABCの外接円の弧AB上に点Pをとり、直線APと辺CBの延長との交点をQ、PCとABの交点をRとします。
において、△ABCはAB＝ACの二等辺三角形であり、∠BAC＝40°になります。△ABCの外接円の弧AB上に点Pをとり、直線APと辺CBの延長との交点をQ、PCとABの交点をRとします。 ∠AQB＝30°であるとき、∠ARCの大きさを求めてください。
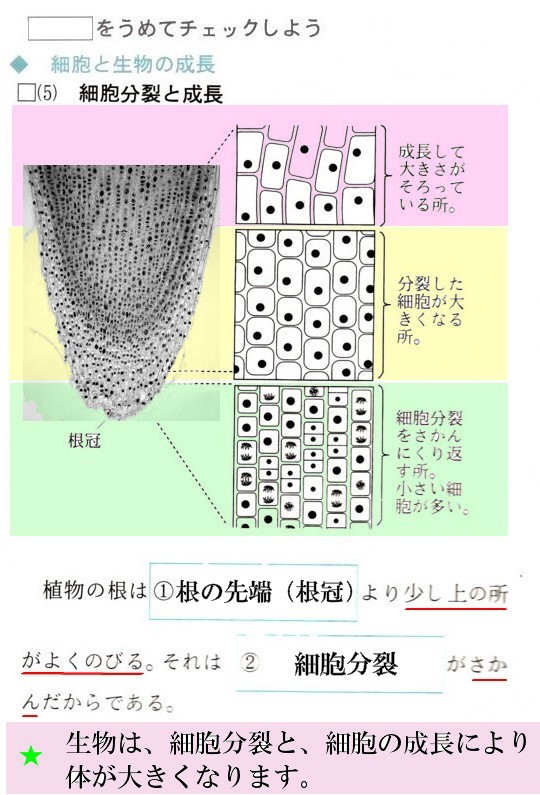
答え
〔証明〕
仮定により
ＡＢ＝ＡＣ
ですから、△ＡＢＣは二等辺三角形になります
二等辺三角形は底角の∠ＡＢＣ＝∠ＡＣＢになります。
∠ＢＡＣ＝40°ですから
底角は
∠ＡＢＣ＋∠ＡＣＢ＝180−∠ＢＡＣ
＝180−40°
＝140°
になり、△ＡＢＣの1つの底角は
140÷2＝70°
になります。
弧ＡＣの円周角はどれも同じになりますから、
∠ＡＢＣ＝70°
∠ＡＰＣ＝70°・・・①
になります。
三角形ＡＰＲで考えます。
＊ △ＡＰＲの∠ＡＰＲと∠ＰＡＲがわかれば、その三角の外角∠ＡＲＣ＝χがわかります。
①は、わかりましたから、
つぎに、∠ＰＡＲを考えます。
∠ＰＡＲは、△ＡＱＢの1つの角になります。
△ＡＱＢの∠ＡＱＢは仮定により
∠Ｑ＝30°
∠ＱＢＡは、180°から∠ＡＢＣを引けばわかりますから、
∠ＱＢＡ＝180°ー∠ＡＢＣ
＝180°ー70°
＝110°
△ＡＱＢの∠ＱＡＢは、
∠ＱＡＢ＝180°ー(∠ＡＱＢ＋∠ＱＢＡ)
＝180°ー（30°＋110°）
＝180°ー140°
＝40°
∠ＱＡＢ＝∠ＰＡＲですから
∠ＰＡＲ＝40°・・・②
△ＡＰＲの2つの内角がわかりました。
①，②より
△ＡＰＲの外角＝∠ＡＲＣで、
∠ＡＰＣ＋∠ＰＡＲ＝∠ＡＲＣ
70°＋40°＝110°
∠ＡＲＣ＝110°
答え ∠ＡＲＣ＝110°
コメント