中学3年数学 関数y=aχ²の値の変化 練習問題9・解答
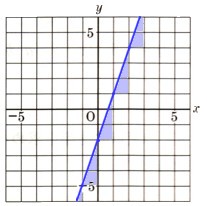
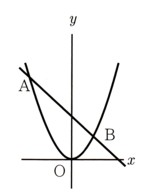
9、次の図 のように、放物線y=2χ²と直線y=−2χ+4が2点A,Bで交わっています。放物線AB上に点Pをとり、△OAB=△PABとなるようにしたい。このとき、Pの座標を求めてください。
のように、放物線y=2χ²と直線y=−2χ+4が2点A,Bで交わっています。放物線AB上に点Pをとり、△OAB=△PABとなるようにしたい。このとき、Pの座標を求めてください。
△OAB=△PAB ということは、
直線ABを底辺と考え、直線ABに平行になる直線を引けば放物線y=2χ²に接します。
その接した部分を点Pと考えます。
この直線y=−2χ+4に平行な直線の式は、
切片は0で、傾きは−2ですから、
y=−2χ になります。
この、y=−2χ+4に平行な直線(y=−2χ)と放物線y=2χ²の接点Pを求めます。
y=−2χ
{
y=2χ²
−2χ=2χ²
χを求めるために二次方程式にします。
2χ²+2χ=0
2(χ²+χ)=0
両辺に1/2をかけます。
χ²+χ=0
かけて0、足して1になる2つの数は
0×1=0、0+1=1
原点Oは0ですから、点Pは1となります。
ただし、χは負の数になりますから−1。
y=−2χにχ=−1を代入します。
y=−2×(−1)
y=2
点Pの座標は(χ、y)=(−1,2)
答え (χ、y)=(−1,2)






コメント