中学３年数学　関数ｙ＝ａχ²の値の変化　練習問題２・解答

中学３年数学　関数ｙ＝ａχ²の値の変化　練習問題２・解答

２、次の問いに答えてください。

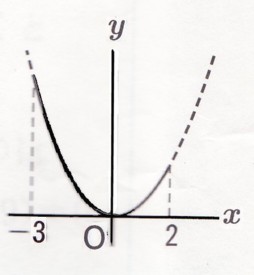
（１）関数ｙ＝χ²で、χの変域が-３≦χ≦２のとき、ｙの変域を求めてください。

ｙ＝χ²　にχ＝−３、χ＝２を代入します。

ｙ＝−３²　、ｙ＝２²

ｙ＝９　　　、ｙ＝４

になります、

ただし、０を挟んでいますから最小はχ＝０になりますから

ｙ＝０ になります。

答え　　０≦ｙ≦９

（２）関数ｙ＝-2χ²で、χの変域が１≦χ≦３のとき、ｙの変域を求めてください。

ｙ＝-2χ²　にχ＝１、χ＝３を代入します。

ｙ＝−２（１²）　、ｙ＝−２（３²）

ｙ＝−２　　　、ｙ＝−１８

今回は０まで行っていません から

ｙ＝−２　になります。

答え　−１８≦ｙ≦−２

（３）関数ｙ＝-χ²で、χの変域が-2≦χ≦４のとき、ｙの変域を求めてください。

ｙ＝-χ²　にχ＝ー２、χ＝４を代入します。

ｙ＝−（−２²）、ｙ＝−（４²）

ｙ＝−４　　　、ｙ＝−１６

今回は０を挟んでいますから、最大はχ＝０ になります。

答え　−１６≦ｙ≦０

（４）関数ｙ＝1/2χ²で、χの変域が-4≦χ≦-1のとき、ｙの変域を求めてください。

ｙ＝1/2χ²　にχ＝−４、χ＝−１　を代入します。

ｙ＝１/2（-4）²、ｙ＝1/2(-1)²

ｙ＝16/2　　　、ｙ＝1/2

ｙ＝８　　　　　、ｙ＝１/2

今回は０を挟んでいませんから、最小は１/２ になります。

答え　１/２≦ｙ≦８