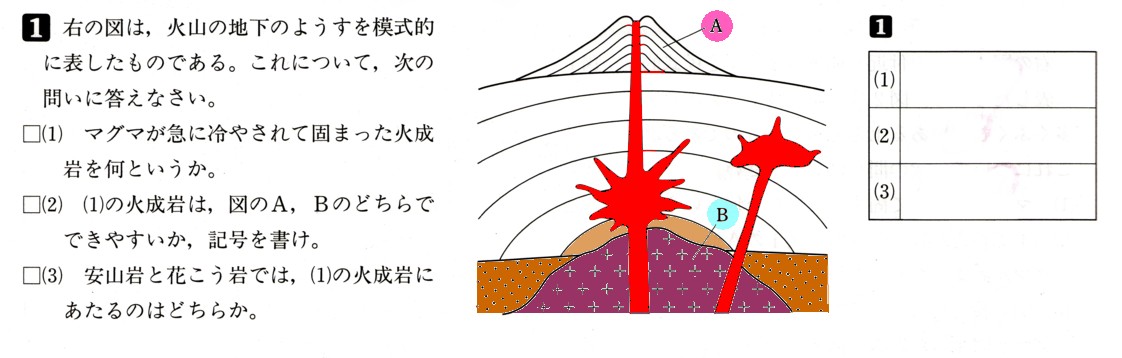
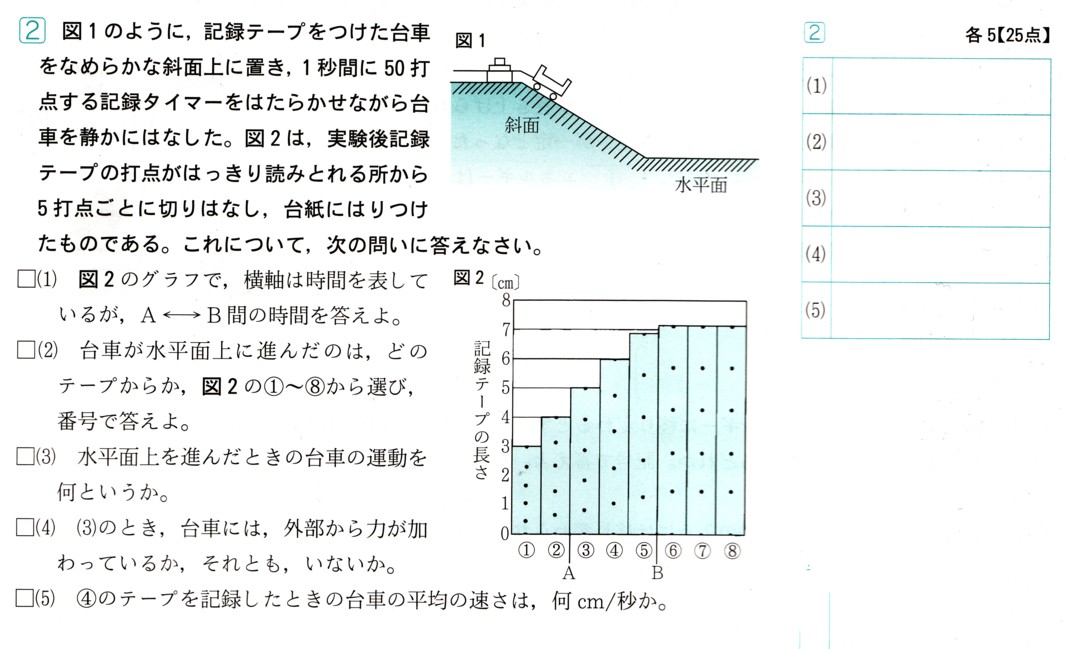
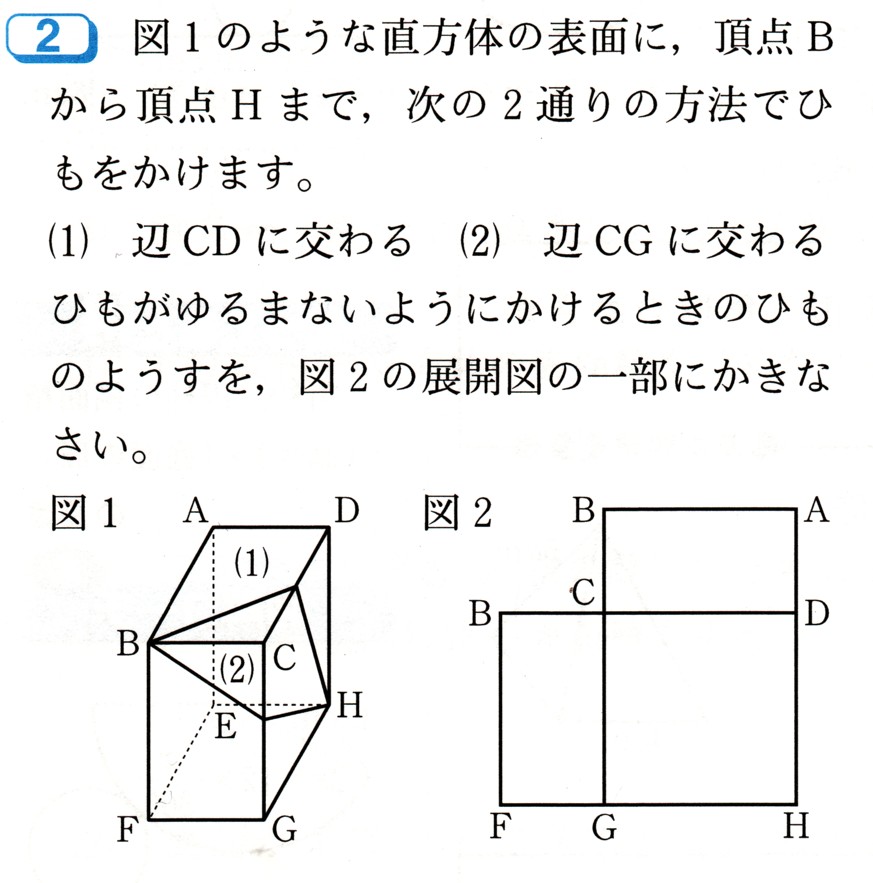
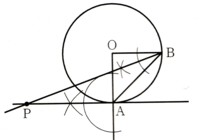
中学２年数学 確率 ２まとめテスト４・解答
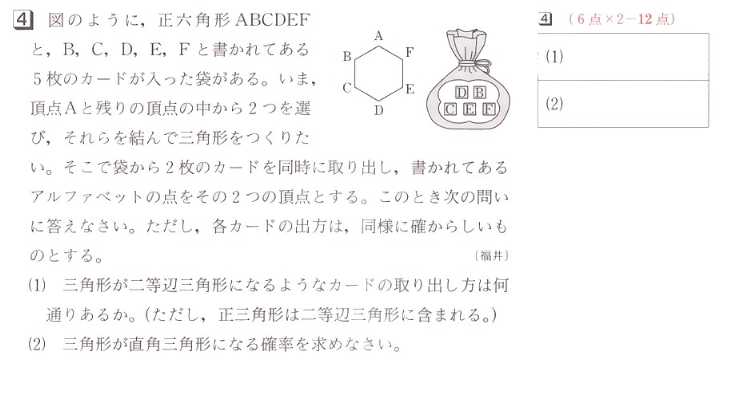
４、図のように，正六角形ＡＢＣＤＥＦと、Ｂ，Ｃ，Ｄ，Ｅ，Ｆと書かれてある５枚のカードが入った袋があります。
いま、頂点Ａと残りの頂点の中から２つを選び、それらを結んで三角形をつくりたい。そこで袋から２枚のカードを同時に取り出しました、
書かれてあるアルファベットの点をその２つの頂点とします。このとき，次の問いに答えてください。
ただし、各カードの出方は、同様に確からしいものとします。
（１）三角形が二等辺三角形になるようなカードの取り出し方は何通りありますか？
（ただし、正三角形は二等辺三角形に含まれます。）
Ａが頂点になる三角形は
１つの角 １つの角
Ｂ Ｃ
Ｂ Ｄ
Ｂ Ｅ
Ｂ Ｆ
Ｃ Ｄ
Ｃ Ｅ
Ｃ Ｆ
Ｄ Ｅ
Ｄ Ｆ
Ｅ Ｆ
の１０通りになります。
この中で，二等辺三角形になるのは，
Ａ（Ｂ、Ｃ）、Ａ（Ｂ、Ｆ）、Ａ（Ｆ，Ｅ）、Ａ（Ｃ，Ｅ）の
４通りになります。
答え ４通り
（２）三角形が直角三角形になる確率を求めてください。
すべての場合は１０通りで、
直角三角形になるには、正六角形の内角の和は
180°×（６−２）＝180°×４
＝720°
１つの内角は720°÷６＝120°
例：
で考えます。
で考えます。 △ＢＣＥにおいて、
正六角形ですから ＢＥ//ＣＤ になり
∠ＣＢＥは、正六角形の１つの内角の二等分線になりますから
∠ＣＢＥ＝120°÷2＝60°・・・１
錯角により、∠ＢＥＣ＝∠ＥＣＤ
△ＤＣＥにおいて
正六角形ですからＣＤ＝ＥＤ
になり△ＤＣＥは二等辺三角形になります。
二等辺三角形の底角はそれぞれ等しくなりますから
∠ＤＣＥ＝∠ＤＥＣ になります。
∠ＣＤＥは、正六角形の１つの内角になりますから
∠ＣＤＥ＝１２０°
∠ＤＣＥ＝∠ＤＥＣ＝３０°
∠ＤＣＥ＝∠ＢＥＣ は錯角ですから
∠ＢＥＣ＝３０°・・・２
１、２より∠ＢＣＥは
∠ＢＣＥ＝１８０ー（６０＋３０）
＝９０
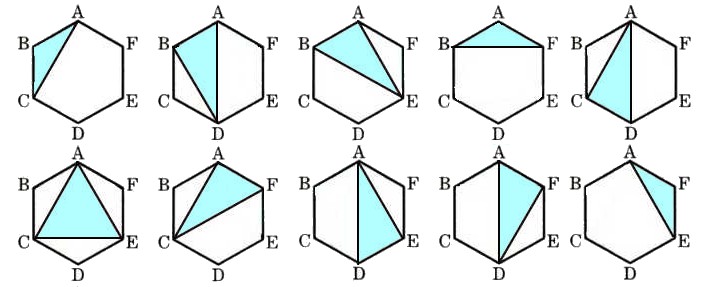
図のような形が直角三角形になります。
のような形が直角三角形になります。 図の中で同じ形を選んでみましょう。
の中で同じ形を選んでみましょう。
は６つあります。 三角形が直角三角形になる確率は
（特定の場合）÷（全部の場合）＝（特定の確率）
６／１０＝３／５
答え ３／５
コメント