中学3年数学 式の展開と因数分解 式の計算の利用 確認問題5・解答
5、半径10㎝の円の半径a㎝長くすると、面積はどれだけ大きくなりますか?
まずは,半径10㎝の円の半径の面積と比べるのですから、半径10㎝の円お面積を求めます。
半径10㎝の円の面積=10²π=10×10×π
=100π㎠
半径10㎝にa㎝ぶん半径を長くするのですから、
(10+a)㎝=半径
(10+a)㎝の円の面積=(10+a)²π
乗法公式を利用します。
●(a+b)²=a²+2ab+b²
(10+a)²π=π(10²+2×10a+a²)
=π(100+20a+a²)
になります。
(10+a)㎝の半径の円と半径10㎝の円の面積とを比べます。
(10+a)㎝の面積は、π(100+20a+a²)㎠
半径10㎝の円の面積は、100π㎠
π(100+20a+a²)ー100π
=100π+20πa+πa²ー100π
=100πー100π+20πa+πa²
=20πa+πa²
=πa(20+a)㎠
答え πa(20+a)㎠








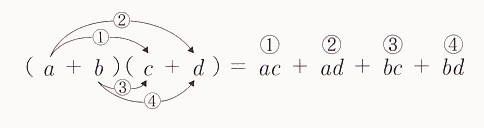






コメント