中学3年数学 関数y=aχ²の値の変化 確認問題3・解答
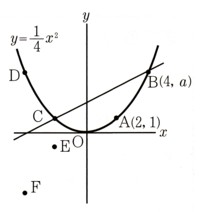
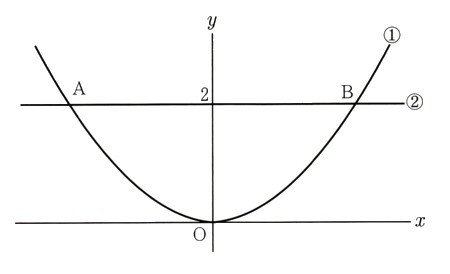
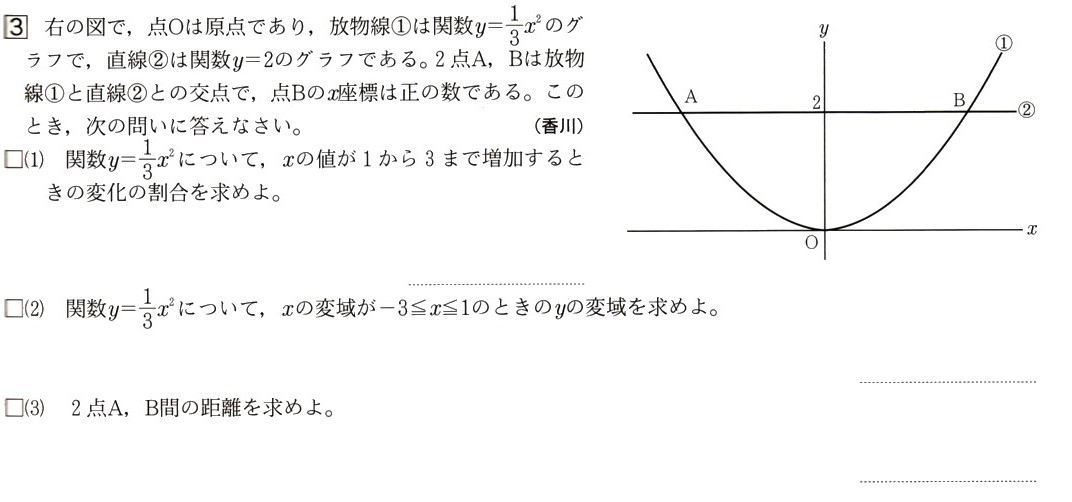
3、次の図 で、点Oは原点になります。放物線?は関数y=1/3χ²のグラフで、直線?は関数y=2のグラフになります。
で、点Oは原点になります。放物線?は関数y=1/3χ²のグラフで、直線?は関数y=2のグラフになります。
2点A,Bは放物線?と直線?との交点で、点Bのχ座標は正の数になります。このとき、次の問いに答えてください。
(1)関数y=1/3χ²について、χの値が1から3まで増加するときの変化の割合を求めてください。
y=1/3χ²にχ=1、χ=3を代入します。
y=1/3(1)²=1/3
y=1/3(3)²=1/3×9=3
yの増加量
変化の割合=―――――
χの増加量
3−1/3 9/3−1/3 8/3 8 1 8 4
――――=―――――=―――=――×―=―=―
3−1 2 2 3 2 6 3
答え 4/3
(2)関数y=1/3χ²について、χの変域が−3≦χ≦1のときのyの変域を求めてください。
y=1/3χ² に χ=−3、χ=1を代入します。
y=1/3(−3)²=1/3×9=3
y=1/3(1)²=1/3×1=1/3
ただし、yの変域は−3~1の間に0を挟んでいますから、最小値は0になります。
0≦y≦3 になります。
答え 0≦y≦3
(3)2点A,B間の距離を求めてください。
y=1/3χ² にy=2を代入します。
2=1/3χ²
χ²=2×3
χ²=6
χ=±√6
Aは、(−√6、2)Bは、(√6,2) になります。
A,B間の距離は√6+√6になりますから、
2√6 になります。
答え 2√6










コメント