中学2年数学 円周角の定理 練習問題１・解答
１、円周角の定理
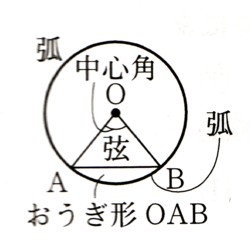
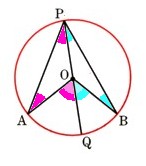
図
のように、、円ＯのＡ⌒Ｂを除いた円周上に点Ｐをとるとき、
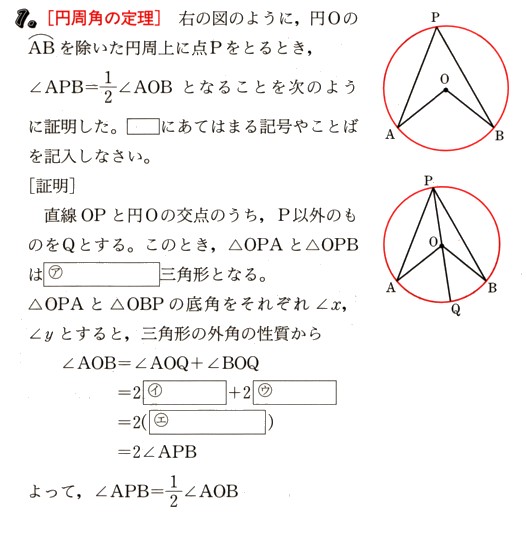
のように、、円ＯのＡ⌒Ｂを除いた円周上に点Ｐをとるとき、 ∠ＡＰＢ＝1/2∠ＡＯＢとなることを次のように証明しました。[ ]にあてはまる記号や言葉を記入してください。
〔証明〕
直線ＯＰと円Ｏの交点のうち、Ｐ以外のものをＱとします。このとき、△ＯＰＡと△ＯＰＢは[ｱ ]三角形となります。
△ＯＰＡと△ＯＢＰの底角をそれぞれ∠χ、∠ｙとすると、三角形の外角の性質から
∠ＡＯＢ＝∠ＡＯＱ＋∠ＢＯＱ
＝2[ｲ ]＋2[ｳ ]
＝2(｢ｴ ｣)
＝2∠ＡＰＢ
よって、
∠ＡＰＢ＝1/2∠ＡＯＢ
〔証明〕
直線ＯＰと円Ｏの交点のうち、Ｐ以外のものをＱとします。このとき、△ＯＰＡと△ＯＰＢは[ｱ 二等辺 ]三角形となります。
△ＯＰＡと△ＯＢＰの底角をそれぞれ∠χ、∠ｙとすると、三角形の外角の性質から
∠ＡＯＢ＝∠ＡＯＱ＋∠ＢＯＱ
＝2[ｲ ∠χ ]＋2[ｳ ∠y ]
＝2(｢ｴ ∠χ＋∠y ｣)
＝2∠ＡＰＢ
よって、
∠ＡＰＢ＝1/2∠ＡＯＢ
答え ア、二等辺 イ、∠χ ウ、∠y エ、∠χ＋∠y
コメント