中学３年数学 式の展開と因数分解 式の計算の利用 練習問題４・解答
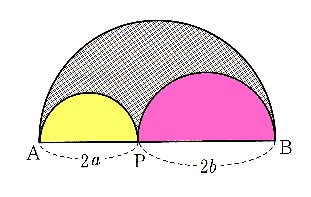
４、図
は線分ＡＢ上に点Ｐをとり、ＡＰ、ＢＰを直径とする半円と、ＡＢを直径とする半円をかいたものになります。ＡＰ＝２ａ、ＢＰ＝２ｂとして、影を付けた部分の面積をａとｂを使って表してください。
は線分ＡＢ上に点Ｐをとり、ＡＰ、ＢＰを直径とする半円と、ＡＢを直径とする半円をかいたものになります。ＡＰ＝２ａ、ＢＰ＝２ｂとして、影を付けた部分の面積をａとｂを使って表してください。 影を付けた部分の面積は、直径ＡＢの半円からから２つの半円を除いた面積になります。
ＡＢの直径の半円をχ
ＡＰの直径の半円をｙ
ＢＰの直径の半円をＺ
としたとき、
影の部分の面積＝χー（ｙ＋Ｚ）
になります。
ｙの面積は（２ａ÷２）×（２ａ÷２）×π＝πａ²／２
Ｚの面積は（２ｂ÷２）×（２ｂ÷２）×π＝πｂ²／２
χの面積は{（２ａ＋２ｂ）÷２}×{（２ａ＋２ｂ）÷２}×π
＝（ａ＋ｂ）²×π／２
（ａ＋ｂ）²×π／２ー（πａ²／２＋πｂ²／２）
＝π（ａ＋ｂ）²／２ー（πａ²／２＋πｂ²／２）
共通因数を探します。
共通因数はπになります。
＝π（ａ＋ｂ）²／２ーπ（ａ²／２＋ｂ²／２）
乗法公式を利用します。
●（ａ＋ｂ）²＝ａ²＋２ａｂ＋ｂ²
＝π（ａ²＋２ａｂ＋ｂ²）／２ーπ（ａ²＋ｂ²）／２
＝π（ａ²＋２ａｂ＋ｂ²ーａ²ーｂ²）／２
＝π（ａ²ーａ²＋２ａｂ＋ｂ²ーｂ²）／２
＝２ａｂπ／２
＝πａｂ
答え πａｂ㎠
コメント