中学1年数学　直線図形と対称　基本の作図　練習問題4　解答・解説

中学1年数学　直線図形と対称　基本の作図　練習問題4　解答・解説

　　次の問いに答えてください

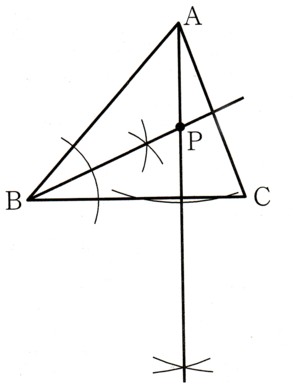
（１）図の、△ＡＢＣでＡから辺ＢＣにひいた垂線と∠Ｂの二等分線の交点Ｐ

　　　を作図してください。

　
　　　　点Ａを中心にした円を、辺ＢＣに接するようにします。

　　　辺ＢＣと点Ａを中心にした円の２つの接点を中心に半径が等しい円を

　　　かきます。その交点と点Ａを直線で結びます。

　　　　これで点Ａから辺ＢＣに垂直な線がひけました。

　　つぎに、∠Ｂの二等分線を作図していきましょう。

　　点Ｂを中心に辺ＡＢ，辺ＢＣに接する円をかきます。

　　その2つの接点を中心に半径が同じの円をかき。その交点と、点Ｂとをつなげた

　　直線をかきます。これで、∠Ｂの二等分線ができました。

　　　2つの直線の交点が点Ｐになります。

　　　　答え　

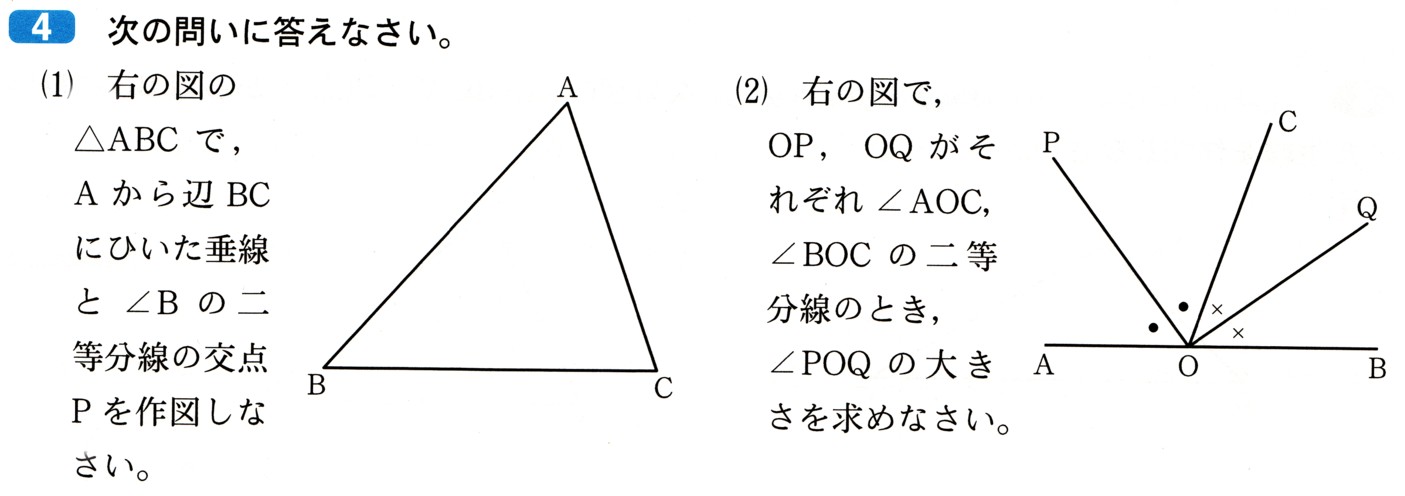
（２）図で、ＯＰ，ＯＱがそれぞれ∠ＡＯＣ，∠ＢＯＣの二等分線のとき、

　　　∠ＰＯＱの大きさを求めてください。

　　　図で考えていきましょう。

　　∠○∠○∠●∠●になっています、この合計は直線ですから180゜になります。

　　ですから、∠○と∠●で180゜の半分の角度になります。

　　　＊∠ＰＯＣ＝Ａ゜、∠ＱＯＣ＝Ｂ゜とすると

　　　　2Ａ＋2Ｂ＝180゜　となります

　　　　∠ＰＯＱ＝Ａ＋Ｂ＝90゜になります。

　　　答え　９０゜