中学2年数学 平面図形 2まとめテスト6・解答
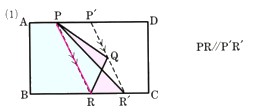
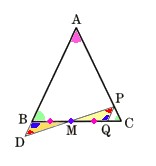
6、 ∠Aを頂角とする二等辺三角形ABCの辺AC上に点Pをとり、PからABに平行な直線を引き、BCとの交点をQとします。また、Pと、BQの中点Mを結んで延長し、ABの延長との交点をDとします。弧のとき、BD=CPであることを証明してください。
∠Aを頂角とする二等辺三角形ABCの辺AC上に点Pをとり、PからABに平行な直線を引き、BCとの交点をQとします。また、Pと、BQの中点Mを結んで延長し、ABの延長との交点をDとします。弧のとき、BD=CPであることを証明してください。
答え 
〔証明〕
△MBDと△MCPにおいて
仮定より
BM=CM・・・?
△ABCは二等辺三角形ですから底角の∠ABC=∠ACB・・・?
仮定によりAB//PQですから
∠BACと∠CPQは同位角により
∠BAC=∠CPQ・・・?
?,?より
 ∠PQMは、△PCQの外角になります。
∠PQMは、△PCQの外角になります。
∠PQM=∠CPQ+∠PCQ・・・?


∠MBDも、△ABCの外角になります。
∠MBD=∠BAC+∠ACB・・・?
?,?より
∠MBD=∠PQM・・・?
∠BМDと∠PMQは対頂角により
∠BМD=∠PMQ・・・?
?、?,?より
3つの角がそれぞれ等しくなりますから
△MBD≡△MCP
になり、
合同な三角形の対応する辺はそれぞれ等しくなりますから
辺BD=辺PQ・・・?
になります。
そして、 △PQCは、?,?より二等辺三角形の頂角を挟む2つの辺の長さは等しくなりますから
△PQCは、?,?より二等辺三角形の頂角を挟む2つの辺の長さは等しくなりますから
二等辺三角形ということがわかります。
PQ=CP・・・?
となり、?,?より
BD=CP
になります。






コメント