スポンサーリンク

中学３年数学　三平方の定理の利用４　確認問題１・解答

三平方の定理
2013.04.16

中学３年数学　三平方の定理の利用４　確認問題１・解答

 

問題はこちらへ

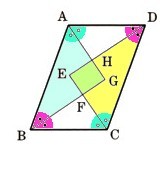
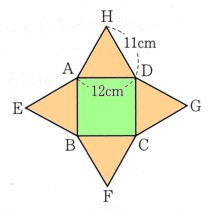
１、上の図は、1辺が12cmの正方形ABCDを底面とし、2辺が11cmの二等辺三角形EBA,FCB,GDC,HADを側面とする四角錘の展開図です。このとき、この四角錘の体積を求めてください。

正四角錐の体積は以下の公式で求められます。

（底面積）×（高さ）×\displaystyle \frac{1}{3}

正方形ABCDの中点をIとします。

（正四角錐の高さ）は△DIEで考えます。

（△DIEの底辺）＝DI

（△DIEの高さ）＝EI

（△DIEの斜辺）＝ED＝11cm

△DIEの底辺を求めるために、△AIDについて考えます。

四角形ABCDは正方形の為、△AIDはIA＝DI、∠AID＝90°の直角二等辺三角形となりますから、三平方の定理を利用します。

（底辺）²＋（高さ）²＝（斜辺）²

直角二等辺三角形の為、底辺＝高さ　となります。

斜辺は12cm、底辺及び高さをxとすると、

\displaystyle 2x^{2}=12^{2} \displaystyle 2x^{2}=144 \displaystyle x^{2}=72 \displaystyle x=6\sqrt{2}\,(x\geq0)

\displaystyle DI=6\sqrt{2}cm

※DBはDIの倍の長さで、DBは直角二等辺三角形BCDの斜辺になるので、

\displaystyle (2x)^{2}=12^{2}+12^{2} \displaystyle (2x)^{2}=2\times12^{2} \displaystyle 2x=12\sqrt{2}\,(x\geq0) \displaystyle x=6\sqrt{2}

と解くこともできます。


（△DIEの底辺）＝\displaystyle 6\sqrt{2}

（△DIEの高さ）＝EI＝x

（△DIEの斜辺）＝ED＝11cm

三平方の定理を利用します。

（底辺）²＋（高さ）²＝（斜辺）²

\displaystyle (6\sqrt{2})^{2}+x^{2}=11^{2} \displaystyle 72+x^{2}=121 \displaystyle 72+x^{2}=121 \displaystyle x^{2}=49

\displaystyle x=7\,(x\geq0)

EI＝7cm

正四角錐の体積を求めるためには、

（底面積）×（高さ）×\displaystyle \frac{1}{3}

（底面積）＝12×12＝144cm²

（高さ）＝7cm

\displaystyle 144\times7\times\frac{1}{3}=336

答え　336cm²

問題はこちらへ

コメント