中学2年数学 図形の調べ方 三角形・多角形と角 確認問題5・解答
５、次の問いに答えてください。
（１）正十角形の内角の和と、1つの内角の大きさを求めてください。
多角形の内角の和を求める式を利用しましょう。
＊（多角形の内角の和）＝180°×（多角形の数−２）
正十角形ですから
（多角形の内角の和）＝180°×(10−2）
＝180°×8
＝1440°
になります。
今回は正十角形ですから、１つの内角は、10分の1になります。
1440°÷10＝144°
になります。
答え 144°
（２）1つの内角の大きさが160°である正多角形は、正何角形になりますか?
今回も正多角形ですから、
（１つの内角）×（多角形の数）＝（正多角形の内角の和）
160°×ｎ ＝160ｎ°＝（正多角形の内角の和）
多角形の内角の和を求める式から、この多角形の角の数を求めます。
（多角形の内角の和）＝180°×（ｎ−2）
になります。
正多角形の内角の和は、160ｎですから、上の式に代入します。
160ｎ°＝180°×（ｎー2）
160ｎ°＝180°ｎー360°
160ｎ°−180ｎ°＝−360°
−20ｎ°＝−360°
ｎ＝18
ｎは、多角形の数になりますから、
１８角形になります、忘れてはいけないのは、今回は正多角形ですから、
答え 正十八角形
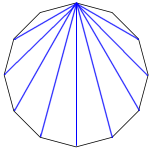
（３）1つの頂点から9本の対角線が引ける正多角形の1つの外角の大きさを求めてください。また、この正多角形では、全部で何本の対角線が引けますか?
まずは、
多角形の角の数を考えます。
多角形の角の数を考えます。 多角形の数は、原点を加えた角に、
引ける線の数に２を加えた数になります。
＊多角形の内角の和を求める式で、
180°×（ｎー２）の（ ）内の−２の部分になります。
１つの頂点か
コメント