中学３年数学 関数ｙ＝ａχ²の値の変化 練習問題３・解答
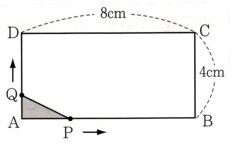
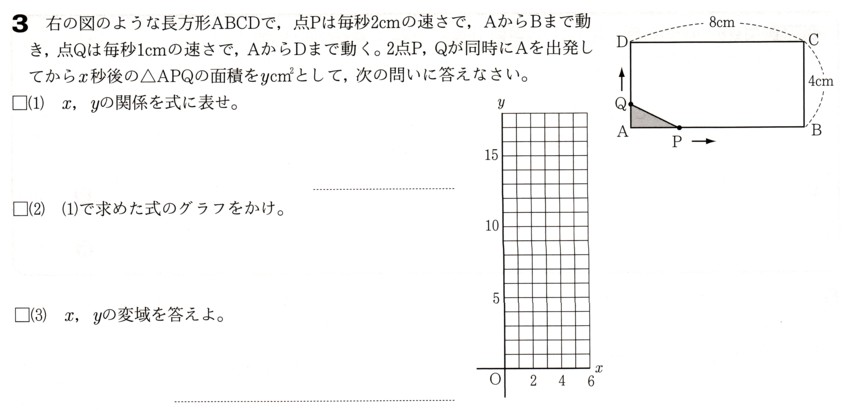
３、図
のような長方形ＡＢＣＤで、点Ｐは毎秒2cmの速さで、ＡからＢまで動きます。点Ｑは毎秒1ｃｍの速さで、ＡからＤまで動きます。
2点Ｐ，Ｑが同時にＡを出発してからχ秒後の△ＡＰＱの面積をｙ㎠として、次の問いに答えてください。
（１）χ、ｙの関係を式に表してください。
△APQの面積の求めかたは、
AP×AQ÷２＝△APQ になります。
APから考えます。
点Pは毎秒2cmの速さで動きますから時間をχとして考えます。
距離＝速さ×時間
（２）×（χ）
AQは、毎秒1cmの速さで動きますから時間をχとして考えると、
距離＝速さ×時間
(１)×（χ）
式にあてはめてみます。
2χ×χ÷２＝ｙ（㎠）
2χ²×1/2＝ｙ（㎠）
χ²＝ｙ（㎠）
答え ｙ＝χ²
（２）（１）で求めた式のグラフをかいてください。
答え 
（３）χ、ｙの変域を答えてください。
点Pは毎秒2cmの速さで、AからBまで動きますから、
ABの長さは８ｃｍですから、
８÷２＝４
４秒でＡ～Ｂまで動きますから点Ｐのχの変域は４までになります。
点Ｑは毎秒１ｃｍの速さで、ＡからＤまで動きますから、
ＡＤの長さは４ｃｍですから、
４÷１＝４
４秒でＡ～Ｄまで動きますから点Ｑのχの変域も４までになります。
ですから χの変域は
０≦χ≦４ になります。
つぎに、ｙ＝χ²の式に０≦χ≦４を代入します。
ｙ＝０、ｙ＝４²＝１６
０≦ｙ≦１６ になります。
答え ０≦χ≦４、０≦ｙ≦１６
コメント