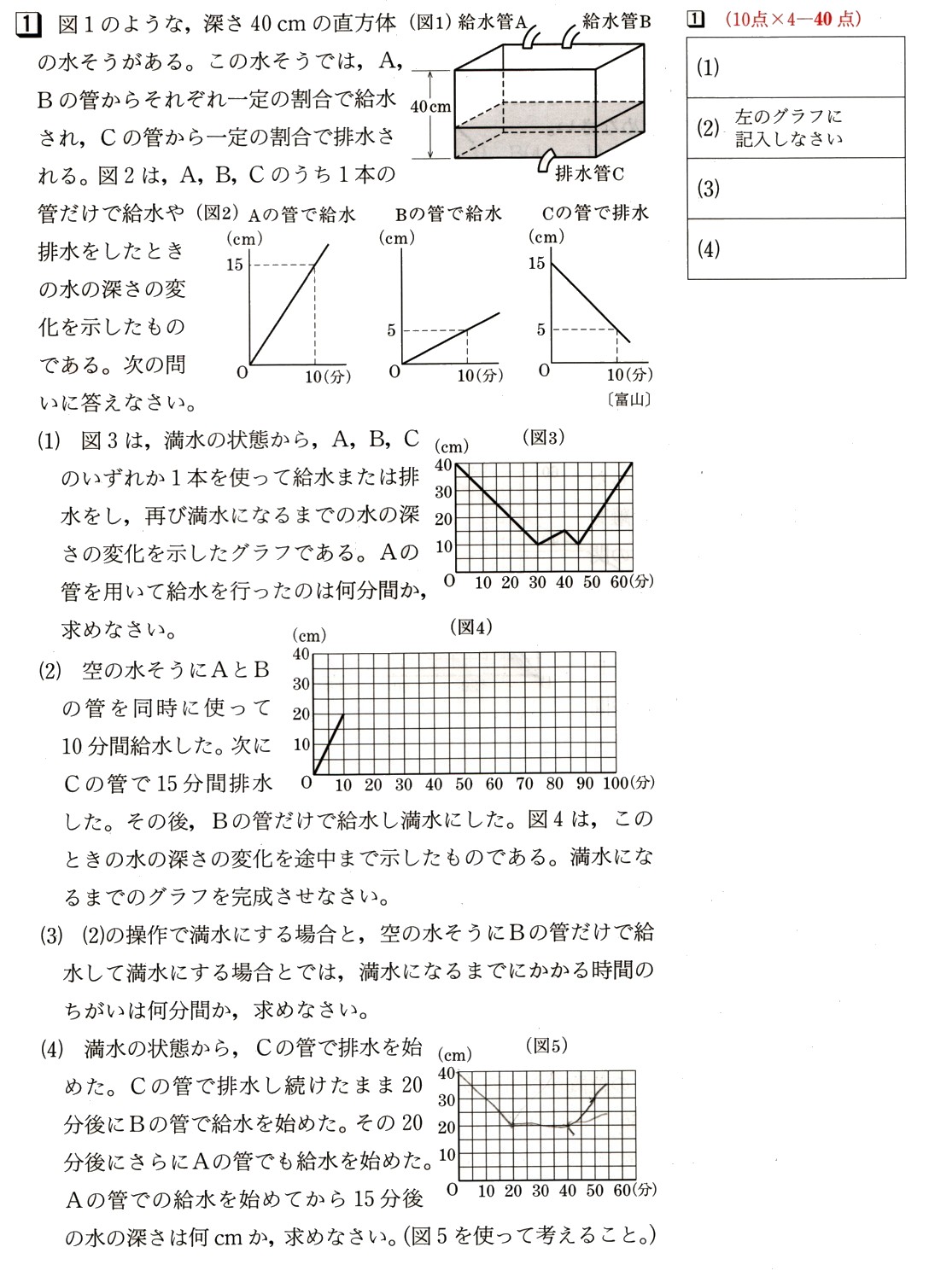
中学2年数学 1次関数 1次関数の応用 確認問題4・解答
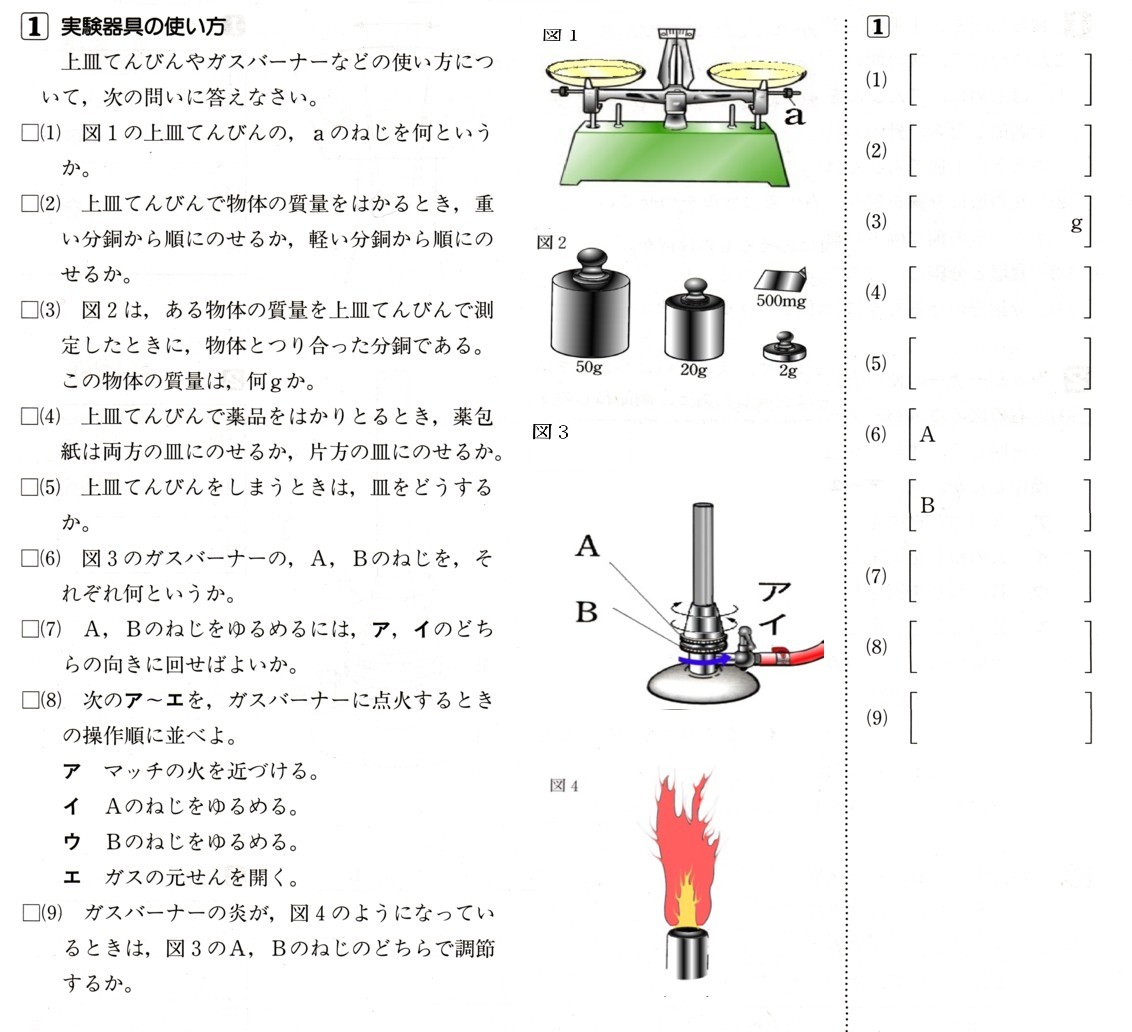
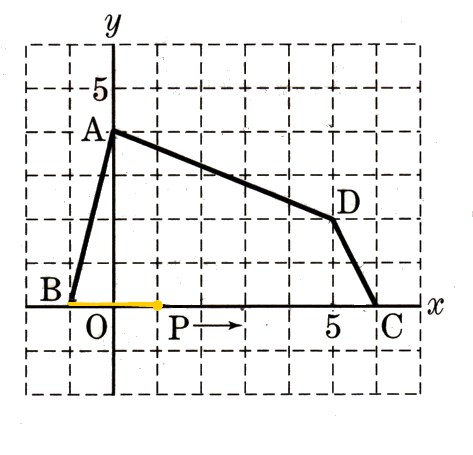
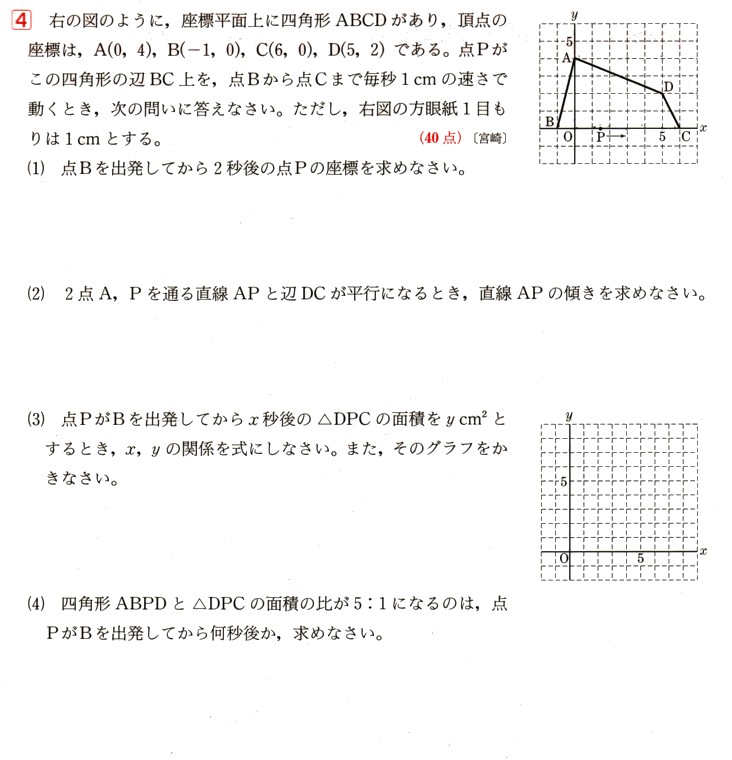
4、図のように、座標平面状に四角形ABCDがあります、頂点の座標は、
A(0,4)
B(−1,0)
C(6,0)
D(5,2)
になります。点Pがこの四角形の辺BC上を、点Bから点Cまで毎秒1cmの速さで動くとき、
次の問いに答えて下さい。
ただし、図の方眼紙1目盛りは1cmとします。
(1)点Bを出発してから2秒後の点Pの座標を求めて下さい。
たずねているのは、距離ですから。
(距離)=(速さ)×(時間)
=(毎秒1cm)×(2秒)
=2cm
方眼の1目盛りが1cmですから、点Pは、点Bから2?のところになります。
答え (χ、y)=(1,0)
(2)2点A,Pを通る直線APと辺DCが並行になるとき、直線APの傾きを求めて下さい。
図を見てください 、辺CDに平行に直線APを引くと、傾きは、どちらも同じです、
、辺CDに平行に直線APを引くと、傾きは、どちらも同じです、
CDの傾きは、右下がりで、χの増加量が−1、yの増加量が2になります。
ですから、
(yの増加量) 2
(傾き)=――――――=−――=−2
(χの増加量) 1
答え 傾き −2
(3)点PがBを出発してからχ秒後の△DPCの面積をy㎠とするとき、χ、yの関係を式にして下さい。また、そのグラフをかいて下さい。
図を見てみると 、△CDPは、0秒から7秒で面積が7㎠→0㎠になります。
、△CDPは、0秒から7秒で面積が7㎠→0㎠になります。
ですから、χの変域は(0≦χ≦7)になります。
三角形の面積は、
(面積)=(底辺)×(高さ)÷2
時間をχとすると、7秒から掛かった時間を引けば、進んだ距離がわかります。
 高さは、点Dと、(5,0)を結んだ長さになりますから、1目盛りが1?ですから、2cmになります。
高さは、点Dと、(5,0)を結んだ長さになりますから、1目盛りが1?ですから、2cmになります。
y=(7−χ)×2÷2
y=−χ+7
y=−(傾き)χ+(切片)
になります。
この式のグラフは、傾きは−1
符号が−ですから、右下がりのグラフになります。
(切片)は+7になります。
(4)四角形ABPDと△DPCの面積の比が 5:1になるのは、点PがBを出発してから何秒後になるのか求めて下さい。
四角形ABPDの面積は、図で 、18㎠ということがわかります。
、18㎠ということがわかります。
5:1になるには、四角形が5/6:△DPCが1/6 になります。
三角形の面積は18㎠の1/6面積になるには、
18/6=3(㎠)
三角形の面積は、
(面積)=(高さ)×(底辺)÷2
高さは、2cmですから、
3=2×χ÷2
χ=3(?)
3?の位置は、点Cからになりますから、
7(?)−3(?)=4(?) の位置になります。
4(?)の位置(距離)は、(速さ)×(時間)
(速さ)=(毎秒1cm)
(4)?=(毎秒1cm)×(時間)
4=1χ
χ=4
χは、(時間)「何秒後」ですから、
答え 4秒後









コメント