中学2年数学　1次関数　1次関数のグラフと式の求め方　確認問題6・解答

中学2年数学　1次関数　1次関数のグラフと式の求め方　確認問題6・解答

６、三角形の底辺をａ?、高さをｈ?、面積をＳ㎠　とすれば、ａ、ｈ、Ｓの間には、Ｓ＝1/2 ａｈ　の関係があります。

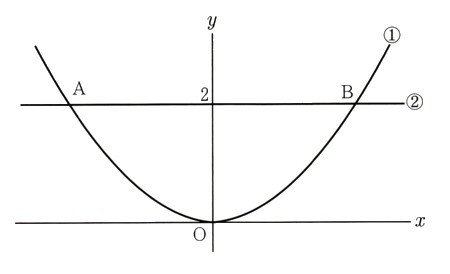
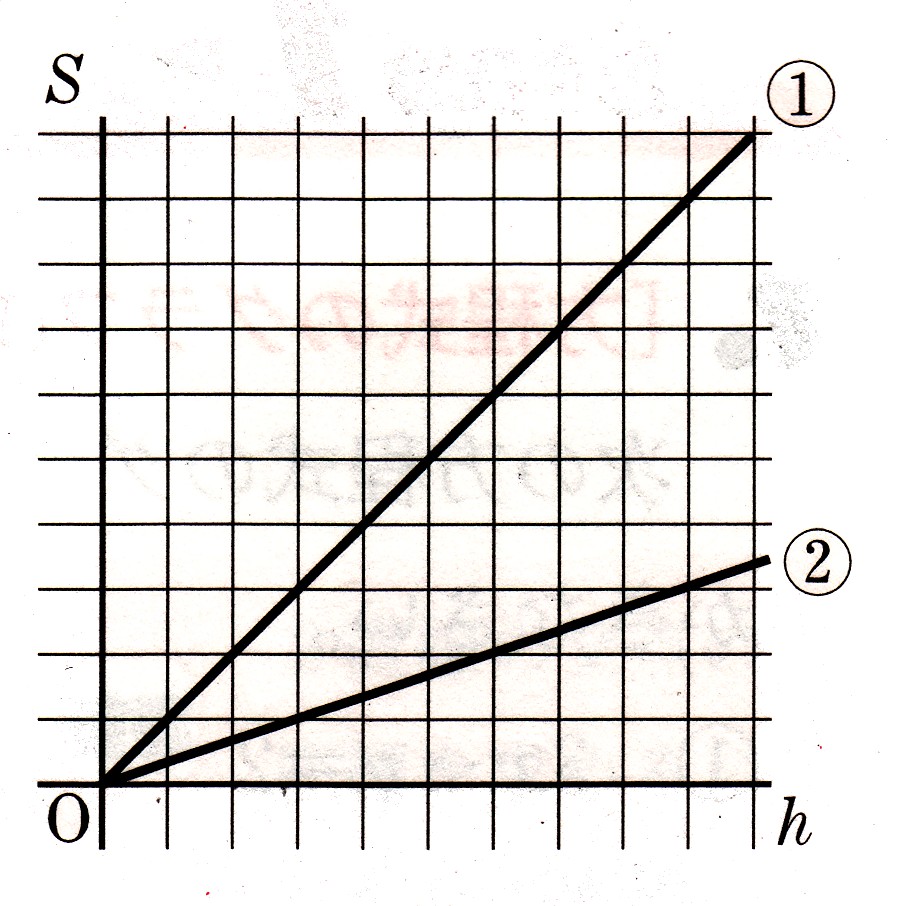
　　ａ＝2のとき、Ｓとｈ　の関係を表すグラフは、図の?のようになります。それでは、Ｓとｈの関係を表すグラフが?のようになるときのａの値はいくらになるのか求めて下さい。

　
　　まずは、このグラフの1目盛りの単位がわかりませんから、

　?のグラフを利用して1目盛りの単位を考えます。

　三角形の面積＝(底辺)×(高さ)÷2

　　Ｓ＝1/2 ａｈ

　になります。

　　底辺＝ａ?

　　高さ＝ｈ?

　　面積＝Ｓ㎠

　　面積＝1/2（底辺）（高さ）

　　になります。

　　　今回は（底辺）が2ですから

　　(底辺)に（２）を代入します。

　　面積＝1/2（２）（高さ）

　　面積＝1×（高さ）

　　面積＝高さ

　　　ですから、1：1　となり、目盛りの単位は(Ｓ軸)＝1,(ｈ軸)＝1

　　になります。

　　グラフから、1次関数の式を作って見ます。

　　ｙ＝aχ＋b

　　面積＝Ｓ㎠＝ｙ

　　高さ＝ｈ?＝χ
　　　　　　　　　　　　　      　　(面積の増加量)
　　1/2(底辺)＝ａ＝「傾き」＝―――――――
　　　　　　　　　　　　　      　　(高さの増加量)

　　[切片は原点Ｏを通っているので、ありません]

　　[面積]＝[(1/2(底辺))]×[(高さ)]

　　と、いうことになります。

　　グラフ?は、ｙ軸(面積)、χ軸(高さ)

　　　　　　  1
　　傾き＝―　＝　1/2(底辺)
　　　　　  　3

　　1/2(底辺)＝1/3

　　(底辺)＝1/3×2

　　(底辺)＝2/3

　　(底辺)＝ａ　ですから、

　　グラフ?　のａ＝2/3　ということがわかりました。

　　　答え　ａ＝2/3