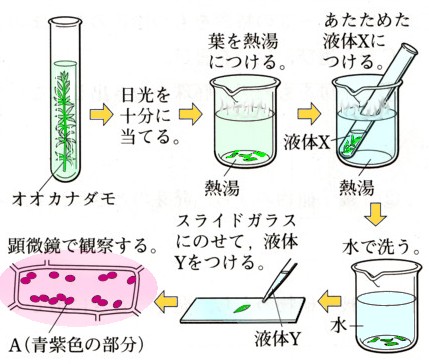
中学1年数学 円とおうぎ形2 練習問題2 解答・解説
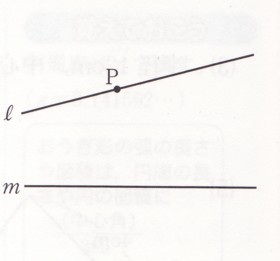
図のように、直径ℓ、mがあり、直線ℓ上に点Pがあります。
次の問いに答えてください。
(1)点Pで直線ℓに接する円の中心は、Pを通る直線ℓの[ ]の上にあります。
[ ]にあてはまることばを答えてください。
接線はその接点を通る半径に垂直になりますから、円の中心は接点を通り
接線に垂直な直線上になります。
答え
垂線
(2)直線m上に中心があり、点Pで直線ℓに接する円Oを作図してください。
点Pが接点になりますから、点Pから直線ℓに垂直にならなければいけません。
そして、円の中点が直線m上にできるようにするには、まず、
直線ℓ上に垂線を作図します。できた垂線と直線mの交点が中心になり、その
中心を中点として点Pまでを半径にした円を作図します。
それでは、作図を考えます。
まず、点Pを中心に適当な円をかき直線ℓとの2つの交点をつくります。
その2つの交点から半径が同じの円をかき、できた2つの交点を直線でつなぎます。
これで、垂線がかけました。つぎに円を作図します。
できた点Pと直線m上の交点をOとして、直線OPを半径にした円を作図します。
これで、完成。
答え 図











コメント